第一章 绪论
- 数字图像处理的概念
- 图像
- 灰度图像是一个二维灰度(或者亮度)函数f(x,y)。
- 彩色图像由三个二维灰度函数组成。
- 数字图像
- 模拟图像:模拟图像可用连续函数来描述。
- 数字图像:空间坐标和灰度(亮度)均用离 散的数字(一般是整数)。
- 像素
- 数字图像是由有限数量的元素组成,每个元素都有特 定的位置(x,y)和幅度f(x,y),这些元素称为像素。
- 图像处理及其相关领域
- 计算机视觉:使计算机来模仿人 的视觉,包括理解并根据视觉输 入采取行动等。属于人工智能的 一个分支。
- 图像理解:用计算机系统解释图 像,就是对图像的语义理解。处 在图像处理和计算机视觉之间。
- 图像
- 数字图像处理的应用实例
- Gamma射线成像
- X射线成像
- 紫外线成像
- 等等
- 数字图像处理的基本步骤
- 图像获取
- 图像增强
- 图像复原
- 彩色图像处理
- 小波变换
- 图像压缩
- 形态学处理
- 图像分割
- 表示与描述
- 目标识别
- 数字图像处理系统的组成
- 由图像输入,图像存储,图像通信,图像处理和分析,图像输出五个模块组成。
心得
这节课主要讲授了这节课的课程及成绩评定等安排,因为今年疫情的影响,所有的教学任务均在线上完成。
这节课也对数字图像有一个概览,了解了它的历史和基础概念,基本步骤,组成及应用。有
第二章 数字图像基础
总结
这一章我们主要学习了6节知识,分别是
- 视觉感知要素
- 光和电磁波谱
- 图像感知和获取
- 我们感兴趣的各类图像都是由“照射源和形成图像的“场景” 元素对光能的反射或吸收相结合而产生的。
- f(x,y) = i(x,y) * r(x,y),其中f(x,y)指的是灰度,i(x,y)是白光强度,r(x,y)是平均反射系数。
- 图像取样和量化
- 为了产生一幅数字图像,需要把连 续的感知数据转化为数字形式,这包括两种处理:取样和量化。取样:图像空间坐标的数字化;量化:图像函数值(灰度值)的数 字化。
- 坐标的数字化称为采样,幅度值的数字化称为量化。
- 采样和量化有两种:均匀的和非均匀的。
- 图像坐标系的表示有三种
- 直角坐标系
- 矩阵坐标系(MATLAB)
- 像素坐标系(用于显示)
- 存储一幅图像所需比特数(bit)𝑏 = 𝑀 × 𝑁 × 𝑘。
- 空间分辨率:图像中可分辨的最 小细节,主要由 采 样间隔值 决定, 采 样间隔值越小,空 间分辨率越高。
- 灰度分辨率是指 灰 度级别中可辨别的 最小变化 ,通常也 把灰度级 L 称为灰 度分辨率。
- 像素间的一些基本关系
- 4领域,8领域,D领域。
- 邻接:位置相近,并且像素值相同或相近。
- 4邻接,8邻接,M邻接,m邻接可以消除8邻接所带来的(通路)二义性。
- 区域:R是图像中 的像素子集。如 果R是连通集,则 称R为一个区域。
- 常见的几种距离度量:
- 欧式距离
- 街区距离。
- 棋盘距离。
- Dm距离。
- 数字图像处理中所用数学操作
- 数组(Array)与矩阵(Matrix)操作
- 线性操作与非线性操作
- 算术操作,加减乘除。
- 集合和逻辑操作:交并补差,与或非、异或。
- 空间操作:单像素操作,领域操作,几何空间操作。
心得
这章我们主要学些了数字图像处理领域的一些基础知识,为以后的深入学习打好一个良好的基础。我觉得这章的引入非常有意思,这个学课是从我们人类感知现实世界的感觉器官入手,然后再进行一个分析和模拟,接入发展为一门学课,这种思想值得我们学习。
可以说,我们计算机这门科学的发展离不开这种思想,很多内容都是将人类的习惯和思维抽象出来,用数学进行解释,然后发展为一门独立的学课,其中包括深度学习,模式识别等等。
这节课的重点是领域的处理方法,因为这是图像最最基础的操作,只有我们打好基础之后,才能对以后的卷积等复杂操作更加熟练。
第三章 灰度变换和空间滤波
总结
这一章我们前三节重点讲了灰度变换,后四节重点讲了空间滤波,主要内容如下:
- 背景知识
- 因为我们想要得到视觉效果更好,或者更有用的图像,所以我们需要进行图像增强。
- 图像增强的基本方法有
- 空间域处理
- 点处理(图象灰度变换、直方图均衡等);
- 邻域处理(线性、非线性平滑和锐化等);
- 频域处理
- 高、低通滤波、同态滤波等。
- 空间域处理
- 空间域图像增强可由下式定义:g(x,y) = T[f(x,y)],其中,T是对f的一种操作,定义在x,y的邻域上。
- 空间滤波用模板来进行卷积,而灰度变换使用灰度变换函数(最小领域为1*1)。
- 基本灰度变换
图像反转
1). 反转公式:
$$ s = L - 1 - r $$
2). 作用:黑变白,白变黑。对数变换
1). 通用形式:
$$ s=c\log _a\left( 1+r \right) \left( a>0 \right) $$幂律(伽马)变换
1). 通用形式:
$$ s=cr^{\gamma} $$
2). 注意 γ<1提高灰度级,γ>1降低灰度级。对比拉伸变换
1). 通用形式:
$$ s=T(r) $$分段线性变换
- 直方图处理
- 直方图是多种空间域处理的基础,直方图操作可用于图 像增强、图像压缩和分割等。
- 有两种直方图,普通的直方图和归一化的直方图。
- 直方图均匀分布时,图像最清晰。
- 直方图均衡化处理: 假设原图的灰度值变量为r,变换后新图的灰度值变量为s,我们希 望寻找一个灰度变换函数T:s=T(r), 使得概率密度函数 pr(r) 变换成均匀分布的概率密度函数 ps(s)。
- 直方图均衡化的灰度变换函数的离散形式为:
$$ s_k=T\left( r_k \right) =\left( L-1 \right) \sum_{i=1}^n{p_r}\left( r_i \right) =\frac{\left( L-1 \right)}{MN}\sum_{j=0}^k{n_j}\text{,}k=0,1,2…,L-1 $$ - 因为直方图是近似的概率密度函数,所以用离散灰度 级进行变换时很少得到完全平坦的结果。
- 变换后灰度级减少,即出现灰度“简并”现象,造成一 些灰度层次的损失。
- 空间滤波基础
- 使用空间模板进行的图像处理,被称为空间滤波。
- 模板本身被称为空间滤波器(也称为空间掩模、 模板、核和窗口)。
- 空间滤波器分为线性空间滤波器和非线性空间滤波器。
- 空间线性滤波的表示:
$$ g\left( x,y \right) =\sum_{j=-a}^a{\sum_{k=-b}^b{w\left( j,k \right) f\left( x+j,y+t \right)}} $$
- 平滑空间滤波器
- 线性滤波器
- 均值滤波器
- 高斯低通滤波器
- 非线性滤波器
- 最大值滤波器
- 中值滤波器
- 最小值滤波器
- 线性滤波器
- 锐化空间滤波器
- 拉普拉斯算子
- 反锐化屏蔽与高频提升滤波
- Robert交叉梯度算子
- Sobel算子
- 混合空间增强法
- 混合空间增强法步骤:
- 拉普拉斯突出图像中的小细节
- 梯度法突出其边缘
- 平滑过的梯度图像用于掩蔽拉普拉斯图像
- 灰度变换增大图像的灰度动态范
- 混合空间增强法步骤:
心得
这章的内容其实我们在数字媒体技术课程中就有过相关了解,不过当时只知其然不知其所以然,只知道某种模板做一种特殊的操作就可以实现一定的图像效果,但是不知道其中的原理,学习完这节课,对以前的一些内容恍然大悟,其实这节课的选修时间放在数字媒体技术之前就好了,因为当时学习数字媒体技术时费了很大的力气才理解了卷积操作和其在编程中是怎样的实现的。
因为一般的理论都是从连续推导,然后继而延伸到离散上,但是如果直接接触离散的话就会一头雾水,为什么要用这几个数,为什么这样可以实现某种效果,这节课对于我受益匪浅。
第四章 频率域滤波
总结
背景
- 任何周期函数都可以表示为不同频率的正弦和或余弦和形式
- 甚至非周期函数也可以用正弦和或余弦乘以加权函数的积分来表示
基本概念
- 复数定义
- 傅里叶变换的基本性质:
- 线性
- 对称性质
- 位移特性
- 尺度变换特性
取样和取样函数的傅里叶变换
- 空间域两个函数乘积的傅里叶变换是两个函数在频率域的卷积。
单变量的离散傅里叶变换DFT
- 离散傅里叶变换(Discrete Fourier Transform,缩写为DFT),是傅里叶变换在时域和频域上都呈离散的形式,将信号的时域采样变换为其DTFT的频域采样。
- 离散(DFT)傅里叶分析方法是信号分析的最基本方法,傅里叶变换是傅里叶分析的核心,通过它把信号从时间域变换到频率域,进而研究信号的频谱结构和变化规律。
两个变量的函数扩展
- 这一节将前面讲的内容扩展到两个变量。
- 图像中的混淆:一般指空间上的混淆,是由欠采样造成的。 主要表现形式是人为引入的缺陷,如线状特征中额锯齿, 伪高光及原图像中不存在的模式的出现。
- 图像重取样:放大看成是过取样,缩小看成是欠取样。
二维离散Fourier变换性质
- 空间域抽样间隔和频域间隔之间的关系:
$$ \Delta \mu =\frac{1}{M\Delta x}\ \ \Delta v=\frac{1}{N\Delta y} $$ - 频移和旋转:用指数项乘以f(x,y)将使DFT的原点移到点(μ0,ν0);反之,用负指 数项乘以F(μ,ν)将使f(x,y)的原点移到点(x0,y0)。
- 旋转特性
- 周期性:只需根据在任一个周期里的N个值就可以从F(u,v)得到f(x,y)。
- 对称性:任意函数可以表示为一个奇数部分和一个偶数部分。实函数的傅里叶变换是共轭对称的。虚函数的傅里叶变换是共轭反对称的。
- 二维循环卷积:
$$ f\left( x,y \right)\bigtriangleup h\left( x,y \right) =\sum_{m=0}^{M-1}{\sum_{n=0}^{N-1}{f\left( m,n \right) h\left( x-m,y-n \right)}} $$
- 空间域抽样间隔和频域间隔之间的关系:
频域滤波基础
频域:频率变量(u,v)定义的空间。
频率域滤波的基本步骤:通过滤波器 函数以某种方式来修改 图像变换,然后通过取 结果的反变换来获得处 理后的输出图像。
大小为M×N的两个函数f(x,y)和h(x,y)的 频率域滤波 表示为: 由卷积定理,该运算对应的空间域运算为:
$$
f\left( x,y \right)\bigtriangleup h\left( x,y \right) =\sum_{m=0}^{M-1}{\sum_{n=0}^{N-1}{f\left( m,n \right) h\left( x-m,y-n \right)}}
$$对比空间域滤波:在M×N的图像f上,用m×n的滤波器进行 线性滤波
$$
g\left( x,y \right) =\sum_{s=-a}^a{\sum_{t=-b}^b{w\left( s,t \right) f\left( x+s,y+t \right)}}
$$
频率域平滑滤波
- 频域低通滤波器:由于噪声主要集中在高频部分,为去除噪声改善 图像质量,滤波器采用低通滤波器来抑制高频成分,通过低频成分,然后再进行逆傅里叶变换获得滤波图像,就可达到平滑图像的目的。
- 常用的频率域平滑滤波器
- 理想低通滤波器(具有振铃现象)
- 巴特沃思低通滤波器(没有振铃效应)
- 高斯低通滤波器
频率域锐化
- 频率域锐化就是为了消除模糊,突出边缘。因此采用高通滤 波器让高频成分通过,使低频成分削弱,再经傅立叶逆变换 得到边缘锐化的图像。
- 频率域锐化滤波器
- 理想高通滤波器
- 巴特沃思高通滤波器
- 高斯高通滤波器
- 频率域的拉普拉斯算子
- 钝化模板、高频提升滤波和高频加强滤波
心得
这章内容我觉得是这节课最难的内容,因为我们计科专业之前没有接触过这部分,也没有学过信号处理,直接铺垫了一些基础知识,就直接讲傅里叶变换,学起来还是比较吃力的,而且这门课的学时又短,在这短暂的时间内完全吃透这部分内容,我觉得还不是很现实,只能利用自己的课下时间,多看看这部分内容,回顾回顾。
第五章 图像复原
总结
图像退化/复原过程的模型
退化:成像过程中的”退化”,是指由于成像系统各种因素的影响, 使得图像质量降低。
引起图像退化的原因:
- 成像系统的散焦
- 成像设备与物体的相对运动
- 成像器材的固有缺陷
- 外部干扰等
图像增强vs图像复原:
- 图像增强的主要目的是提高图像的可懂度,而图像复原的目的是提高图像的逼真度。
- 图像增强的方法为空间域和频率域法,而图像复原的方法为线性复原方法。
- 图像增强不考虑降质的原因,而且不一定要去逼近原图像,而图像复原要建立降质模型,有客观标准,是客观过程。
- 二者(图像复原与增强)的目的都是为了改善图像的质量。如果图像已退化,应先作复原处理,再作增强处理。
退化图像描述:
$$ g\left( x,y \right) =h\left( x,y \right) *f\left( x,y \right) +\eta \left( x,y \right) $$
噪声模型
- 重要的噪声:
- 高斯噪声
- 瑞利噪声
- 伽马噪声
- 指数分布噪声
- 均匀分布噪声
- 脉冲噪声
- 一些重要的噪声概率密度函数
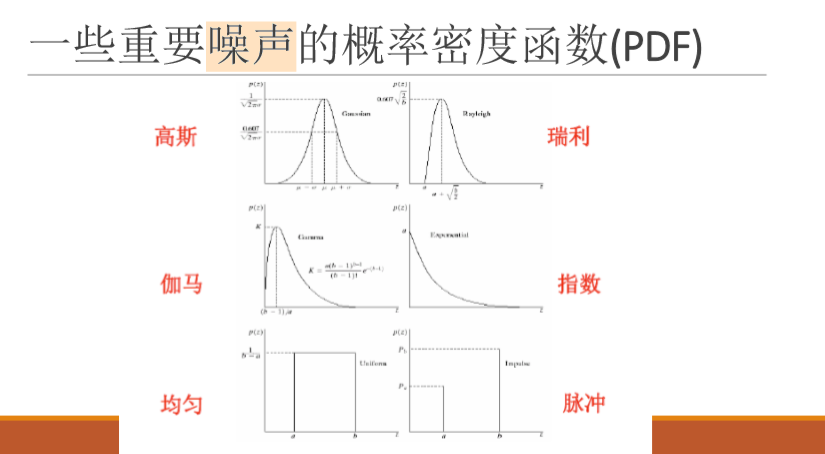
- 几种噪声的应用
- 高斯噪声源于电子电路噪声和由低照明度或高温带来 的传感器噪声
- 瑞利噪声对分布在图像范围内特征化噪声有用
- 伽马分布和指数分布用于激光成像噪声
- 均匀密度分布作为模拟随机数产生器的基础
- 脉冲噪声用于成像中的短暂停留中,如错误的开关操 作
- 重要的噪声:
空间域滤波复原
以下均运用仅有噪声的复原——空间滤波:- 均值滤波器
算术均值滤波器、几何均值滤波器、谐波均值滤波器、 逆谐波均值滤波器 - 顺序统计滤波器
中值滤波器、最大值滤波器、最小值滤波器、中点滤波器、 修正后的Alpha均值滤波器 - 自适应滤波器
自适应局部噪声消除滤波器、自适应中值滤波器
- 均值滤波器
频率域滤波复原
- 带阻滤波器:阻止一定频率范围内的信号通过而 允许其它频率范围内的信号通过 。
- 理想带阻滤波器
- 巴特沃思带阻滤波器
- 高斯带阻滤波器
- 带通滤波器:允许一定频率范围内的信号通过而组织其它频率范围内的信号通过。
- 带通滤波器执行与带阻滤波器相反的操作。
- 不直接使用,损失大量图像细节。
- 可利用带通滤波器提取噪声模式。
- 陷波滤波器:阻止(或通过)事先定义的中心频率邻域内的频率。
- 理想陷波滤波器
- 巴特沃思陷波滤波器
- 高斯陷波滤波器
- 带阻滤波器:阻止一定频率范围内的信号通过而 允许其它频率范围内的信号通过 。
图像退化
心得
其实图像复原我们是在之前的选修课中接触过的,之前我们已经实现了图像去雾,这就图像复原的一种,利用了一定的先验知识,将图像的“退化”逆退化,得到退化前的图像。图像复原在生活中是非常需要的一种技术,因为传感器噪声,摄像机聚焦不佳、物体与摄像机之间的相对移动、随机大气湍流、光学系统的象差、成像光源和射线的散射等都会造成图像退化,而如何得到复原图像,就是值得研究的一个课题了。
与之对比的是图像增强,图像增强更注重的是主观感受,而图像复原就注重客观过程了,我个人觉得图像复原的过程比较苦难一点,因为退化过程如果不能找到一个很好的机理的话,图像复原是比较困难的。
第六章 彩色图像处理
总结
概述
- 人眼的机理和照相机类似,瞳孔相当于照相机光圈的作用,晶状体相当于透镜,而视细胞可以检测亮度和颜色。
- 锥状细胞将电磁光谱的可见光部分分为三个波段,红,绿,蓝。
- 所有的颜色都可以看作是这三种颜色按照不同的比例混合而成的。
- 人眼成像过程:视细胞受到光刺激产生电脉冲——>视神经中枢——>大脑成像。
颜色基础
- 彩色光谱可以分为6个宽的区域;紫色,蓝色,绿色,黄色,橘红色和红色。
- 可视光区的波长在400nm-700nm,当光谱采样限制到三个人类视觉系统敏感的红绿蓝光波段时,对这三个光谱带的光能量进行采样,就可以得到一副彩色图像。
- 人眼所感知到的物体的颜色由物体的反射光的特性所所决定。
- 颜色的特性:亮度,饱和度,色调。
颜色模型
颜色模型(色彩空间)是为了按照某种标准来指定颜色。
颜色模型的设计通常是为了便于硬件实现或者对颜色的控制。
RGB模型
- 在彩色显示器,彩色摄像机中广泛使用。
- 建立在笛卡尔坐标系中。
- 在RGB空间中,用于表示每一像素的比特数称位像素深度。
- 24比特深度的图像通常称位i全彩色或者真彩色图像。
CMY和CMYK模型
- 颜料三原色:青,品红,黄。
- 适用于彩色答应,印刷行业,为减色模型。
HSI彩色模型
- HSI模型与人眼对颜色的描述很相似,H为色调,S为饱和度,I为强度/亮度/灰度。
以上三种色彩空间都可以进行一定的相互转换。
全彩色处理
- 彩色图像增强
- 其实就是对彩色图像的三个通道进行一定的增强,增强方法相同。
- 彩色图像复原
- 将第五章的单色图像复原技术直接推广到彩色图像,分别作用于三个通道,即可进行彩色图像复原。
- 彩色图像分析
- 彩色图像分割方法=单色图像分割方法+色彩空间。
- 彩色图像增强
伪彩色处理
- 伪彩色处理是指将黑白图像转换为彩色图像,或者是将单色图像变换给定彩色分布的图像。
- 主要目的是提高人眼对图像细节的分辨能力,以达到图像增强的目的。
- 基本原理是将黑白图像的各个灰度级匹配到色彩空间中的一点,从而使单色图像映射为彩色图像。
- 映射方法:
- 密度分层法
- 灰度级-彩色变换法
- 频率域滤波法
- 映射原理:
$$
R\left( x,y \right) =f_R\left[ f\left( x,y \right) \right]
$$
$$
G\left( x,y \right) =f_R\left[ f\left( x,y \right) \right]
$$
$$
B\left( x,y \right) =f_R\left[ f\left( x,y \right) \right]
$$
彩色变换
- 这里的彩色是相对于第三章的灰度变换而言的,而不是指色彩空间的变换。
- 与灰度变换的区别在于,此时f(x,y)是以一个向量,有三个分量。
- 灰度反转,对数变换,幂律变换可以直接用于处理RGB分量。
- 分段线性变换,直方图均衡,直方图拉伸不能直接处理RGB分量的方式进行。
- 直方图处理需要将RGB转换为HSI,然后对I分量进行处理,而HS分享保持不变,之后将HSI转换为RGB。
心得
这节课内容我们在数字媒体技术中也有所涉及,但是没有这么深入浅出的讲解,这节课使我们对当时的图像色彩空间转换有了一个更深入的了解。其实这节课主要是将之前所学的知识拓广到彩色图像,而彩色图像可以看作多通道的单色图像,只是将方法分别用于通道即可,而有些方法需要变换色彩空间进行处理(彩色图像的直方图处理),这是值得注意的。
另外,市面上有着黑白图像转彩色图像,我想就是运用了这里的伪彩色图像技术,可以看到理论知识明显有着应用场景,这可能也是我们学科的特点吧,由应用场景提出需求,然后用理论分析后解决需求。
第九章 形态学图像处理
总结
数学形态介绍
- 形态学:通常指生物学中对动植物的形状和结构进行研究的一个 分支。
- 数学形态学(Mathematical Morphology)是分析几何形状和结构的数 学方法,它建立在集合代数的基础上,是用集合论方法定量描述目标几 何结构的学科。
- 基本思想:利用一个结构元素(相当于模板)去探测一个图像,看是否能将这个结构元素 很好地填放在图像的内部,同时验证填放结构元素的方法是否有效。
- 形态学图像处理表现为一种邻域运算形式。
- 形态学运算的效果取决于结构元素的大小、形状以及逻辑运算的性质。
- 用途:简化图像数据,保持它们基本的形状特性,并除去不相干的结构
- 基本的运算包括: 二值腐蚀和膨胀、二值开闭运算。
- 结构元素:结构元素对数学形态学的运算结果有决定性的作用。
- 形态学图像分析有一些明显的优势,比如在恢复处理中,并行处理中都有明显的优势。
数学基础
集合论基本概念
- 属于,不属于,空集
- 子集, 交集,并集
- 互斥,补集,差集
集合关系的图形表示
集合的反射
集合的位移
二值图像的逻辑运算
形态学基本运算
膨胀
使图像扩大,也就是用B的反射进行平移与A的交集不能为空
每当结构元素 在目标图像A上平移后,结构元素 与其 覆盖的子图像中至少有一个元素相交时,就将目标图像中与结构 元素 的原点对应的那个位置的像素值置为“1”,否则置为0。
结构元素对膨胀运算的影响
- 当目标图像不变,但所给的结构元素的形状改变时。
- 结构元素的形状不变,而其原点位置改变时,膨胀元素那的结果会发生改变。
膨胀运算的应用:
- 利用膨胀运算将相邻的物体连接起来
- 利用膨胀运算填充目标区域中的小孔
腐蚀
- 腐蚀:使图像缩小,B移动后完全包含在A中时,B的原点位置的集合
- 腐蚀运算的实质就是在目标图像中标出那些与结构元素相同的子图像 的原点位置的像素。
- 腐蚀运算的应用:
- 利用腐蚀算法消除物体之间的粘连示例
- 利用腐蚀算法识别物体示例
- 腐蚀和膨胀的一些属性:
- 平移不变性
- 顺序不变性
- 增加算子
- 比例不变性
- 对偶性
开和闭
- 开操作一般使对象的轮廓变得光滑,断开狭窄的间断和消除细的突出物。
- B对A进行的开操作就是先用B对A腐蚀,然后用B的结果进行膨胀。
- 闭操作通常狭窄的间断和细长的“鸿沟”,消除小的孔洞,并填补轮廓线的缝隙。
- B对A进行的闭操作就是先用B对A膨胀,B对结果进行腐蚀。
- 开操作和闭操作也是一对关于集合求补及映射的对偶操作。
- 形态学滤波:先开后闭
- 击中与否变换
二值形态学图像处理
- 形态学的基本应用是提取对形状表示和描述有用的图像元素。
- 边界提取。
- 区域填充
- 连通分量提取
- 细化
- 粗化
心得
这节课的理论知识说实话不难,但是其应用还得好好钻研钻研,毕竟我们已经学过一些离散数学的知识,所以再接触这章时已经有了相应的背景知识,不至于学起来太困难。
欢迎在评论区中进行批评指正,转载请注明来源,如涉及侵权,请联系作者删除。

