00Leetcode刷题总结

0开发 > Z刷题 Java

发布时间 : 2021-12-20 22:28

字数:3.7k 阅读 :

Leetcode刷题总结

方法论

我们做某道题, 不是把这道题做出来, 而是形成一套系统的方法论, 按方法论解决问题, 比如”正则表达式”半个小时没做出来, 有样例错了, 此时就应该看答案, 我们学的是动态规划, 是算法, 不是真正的解决某道题, 就算现在能解决, 没有形成算法思想的话, 也无以为继.

先看数据量或者时间空间复杂度要求, 通过数据量判断什么或者导向算法方向.
注意乘法或者数据范围, 要用Int, 还是Long, 还是Long Long
要考虑边界条件

ACM模式

导包

import java.math.BigInteger;
import java.util.Scanner;
import java.util.*;

模板

public class Main {
    //输入输出函数
    private static void inOut() {

    }
    //核心代码函数
    private static void func() {

    }
    //主函数调用函数,核心代码函数被输入输出函数调用,所以主函数只调用输入输出函数
    public static void main(String[] args) {
        inOut();
    }
    
}

编程素养

代码规范

int i, j;
int i = i + 1;
for (int i = 0; i < len; i++) {
    int arrIndex = 1;
    if(arrIndex == i) {
        ...
    }
}

库函数使用

如果题目关键的部分直接用库函数就可以解决，建议不要使用库函数。

如果库函数仅仅是解题过程中的一小部分，并且你已经很清楚这个库函数的内部实现原理的话，那么直接用库函数。但是要注意库函数带来的复杂度的影响

常用类操作

BigInteger

BigInteger bigNum = new BigInteger("12345");      //BigInteger(String val) 
        BigInteger bigNumTwo = new BigInteger("2");      //BigInteger(String val) 

        //加法
        bigNum.add(bigNumTwo);

        //减法
        bigNum.subtract(bigNumTwo);

        //乘法
        bigNum.multiply(bigNumTwo);

        //除法
        bigNum.divide(bigNumTwo);

        //一些常量
        // BigInteger.ZERO;
        // BigInteger.ONE;
        // BigInteger.TEN;

        //常见运算
        bigNum.max(bigNumTwo);
        bigNum.min(bigNumTwo);
        bigNum.mod(bigNumTwo);

        //返回对应的整数
        bigNum.intValue();
        
        //返回对应数字的大数
        BigInteger.valueOf(123);

StringBuilder

//构造
StringBuilder res = new StringBuilder();
StringBuilder res = new StringBuilder(int capacity) 
StringBuilder res = new StringBuilder(String str) 

//末尾添加字符
res.append('c');

//插入字符
res.insert(0, 'c');

//改变字符
res.setCharAt(0, 'c');

//得到字符
res.charAt(0);

//删除字符
res.deleteCharAt(0);

//反转字符返回StringBuilder
res.reverse();

//转化为String()
res.toString();

String

常用函数

返回值	函数体	说明
	`String(char[] value)`	构造函数
	`String(StringBuilder builder)`
`char`	`charAt(int index)`
`int`	`compareTo(String anotherString)`	相等返回0, 前者比参数小返回负数, 否则返回正数
`int`	`compareToIgnoreCase(String str)`	按字典序比较忽略大小写
`String`	`concat(String str)`	也可以用`+`号来拼接
`int`	`indexOf(int ch)`	返回字符`ch`第一次出现的位置
`int`	`indexOf(String str)`	返回子串第一次出现的下标
`int`	`length()`	返回长度
`boolean`	`matches(String regex)`	是否包含`regex`表达式的字符串
`String`	`replace(char oldChar, char newChar)`
`String []`	`split(String regex)`
String	`substring(int beginIndex, int endIndex)`
`char[]`	`toCharArray()`
`String`	`trim()`	删除首尾空白符
`String`	`valueOf(char c)`	返回这个`c`的字符串,重载还可以是`double`, `float`, `int`, `Object`

迭代访问String

//方法一:
String str = "asdfghjkl";
for(int i=0;i<str.length();i++){
    char ch = str.charAt(i);
}
//方法二:
char[] c=s.toCharArray();
for(char cc:c){
  ...//cc直接用了
}

空字符串 vs null串

null串的判别方法:

 if (str == null);

空字符串的判别方法

if (str.length() == 0);
if (str.equals(""));

注意的是,

String b = s.substring(s.length(), s.length());//返回的是空字符串.

List

List的初始化

//第一种, 空List然后添加值
List<Integer> l = new ArrayList<>(5);//这样不能初始化5个大小的List, 也就是不能l.set(3, 5)这样使用
l.add(1);

//第二种, 用一些值来初始化
List<String> l = new ArrayList<>(Arrays.asList("1", "2", "3"));

List不能用[ ]访问.

        //构造
        List<Integer> ans = new ArrayList<>();
        
        //添加元素
        ans.add(5);
        
        //插入元素, 注意是add
        ans.add(0, 5);

        //得到
        ans.get(0);

        //移除某个位置
        ans.remove(0);

        //设置
        ans.set(0, 5);

        //长度
        ans.size();

        //排序
        ans.sort();

Stack

        //构造
        Stack<Integer> ans = new Stack<>();

        ans.push(0);

        int top = ans.peek();

        top = ans.pop();

        //是否为空
        ans.empty();

Queue

        //构造
        Queue<Integer> que = new LinkedList<>();

        //队尾添加
        que.offer(1);

        //队头取但不出队
        que.peek();

        //出队头并取队头
        que.poll();

        //去长度
        que.size();

PriorityQueue

        //构造
        PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>(){  
            public int compare(int[] pair1, int[] pair2) {
                return pair1[0] != pair2[0]?pair2[0]-pair1[0]:pair2[1]-pair1[0];//语法
            }
        });

        pq.offer(new int[]{1,1});

        pq.peek();

        pq.poll();

        //pq.contains()判断是否含有某个元素

        pq.size();

Set

实现类

HashSet: 无序, 基于 HashMap实现.
LinkedHashSet: HashSet的子类, 基于LinkedHashMap实现.
TreeSet: 有序, 基于红黑树实现

常用操作

返回值	函数体	说明
`boolean`	`add(E e)`	`e`以前不在集合中的符话返回真
`boolean`	`addAll(Collection<? extends E> c)`
`void`	`clear()`	清空
`boolean`	`contains(Object o)`
`boolean`	`containsAll(Collection<?> c)`
`boolean`	`equals(Object o)`
`boolean`	`isEmpty()`
`boolean`	`remove(Object o)`	如果包含`e`的话返回真
`boolean`	`removeAll(Collection<?> c)`
`int`	`size()`
`Object[]`	`toArray()`	collection.toArray()是旧式的获得对象数组的方法。
`<T> T[]`	`toArray(T[] a)`	String a[] = collection.toArray(new String[0]);

遍历

set遍历不能使用for循环+set[i]的方法遍历,而用以下方法遍历:

//方法一, 迭代器
Iterator it1 = set.iterator();
while(it1.hasNext()) {
    System.out.println(it1.next());
}

//方法二, 迭代器for循环
for(Iterator it2 = set.iterator(); it2.hasNext();) {
    System.out.println(it2.next());
}

//方法三, 加强for
for(Integer item:set) {
    System.out.println(item);
}

Map(Interface)

实现类: HashMap,

常用操作

返回值	函数体
`boolean`	`containsValue(Object value)`
`boolean`	`containsKey(Object key)`
`V`	`get(Object key)`
`V`	`put(K key, V value)`
`int`	`size()`

循环遍历

Map<Integer, Integer> map = new HashMap<Integer, Integer>();
 
for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
 
    System.out.println("Key = " + entry.getKey() + ", Value = " + entry.getValue());
 
}

一维数组Map

List<Map<Character, Boolean>> row = new ArrayList<>();
for (int k = 0; k < 9; k++) {
    row.add(new HashMap<>());
}
row.get(i).put(board[i][j], true);//置放值.

二维数组Map

List<List<Map<Character, Boolean>>> nine_Square = new ArrayList<>();
for (int i = 0; i < 3; i++) {
    List<Map<Character, Boolean>> temp = new ArrayList<>(3);
    for(int j = 0; j < 3; j++){
        temp.add(new HashMap<Character, Boolean>());
    }
    nine_Square.add(temp);
}
nine_Square.get(i/3).get(j/3).put('c', true);//置放值

TreeMap

平衡树, 会自动以key从小到大排序

        //构造
        //TreeMap(Map<? extends K,? extends V> m)
        TreeMap<Integer, Integer> tm = new TreeMap<>();                
         
        //添加元素
        tm.put(0, 5);

        //得到元素
        tm.get(0);

        //删除key-value
        tm.remove(0);

        //得到长度
        tm.size();

        //最高的(最后的)
        tm.lastKey();

        //最低的
        tm.firstKey();

位运算

<<左移, 低位补0

>>右移, 正数高位补0, 负数高位补1

>>>无符号右移, 高位补0

& 位与, n&1可以得到n的最低位的数字为0还是为1

|, 位或, n|1和n|0, 如果n的最低位是0的话, 那么会将n的最低位置为1或0.

^ 位异或

~ 位非, 一元运算符

&= 按位与赋值

|= 按位或赋值

^= 按位非赋值

>>= 右移赋值

>>>= 无符号右移赋值

<<= 赋值左移

和 += 一个概念而已。

Arrays

操作:

常用实现类
添加元素
删除元素
遍历

Collection⏲

Arrays⏲

Stream流

java中常用数据结构和对应数组的转化

int[] 转list

 List<Integer> a1 = Arrays.stream(nums1).boxed().collect(Collectors.toList());

list转int[]

int []result = new int[list.size()]
for (int i =0; i < r.size(); i++) {
    result[i] = list.get(i);
}

char转int(0-9)

char c = '9';
int num = c-'0';

int 转char(0-9)

int num = 0;
char c = num + 48;//'0'的ASCII码是48, 'A'为65, 'a'为97

list 转set

//list转set
Set<String> set = new HashSet<>(set);

set转list

List<String> list = new ArrayList<>(set);

Array转list

String[] s = new String[]{"A","B"};
List<String> list = Arrays.asList(s);

List转Array

String[] dest = list.toArray(new String[0]);//new String[0]是指定返回数组的类型
System.out.println("dest: " + Arrays.toString(dest));

String转int

    1、 int i = Integer.parseInt([String]); 
    2、 int i = Integer.valueOf(my_str).intValue();

递归

我觉得递归要明确三件事

函数实现了什么功能, 返回值是什么, 传递的参数是什么.
终止条件是什么(只需要考虑最简单的情况即可, 不要想太深)
写非终止条件下的情况,

比如

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/insert-into-a-binary-search-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

代码

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        //函数功能, 给以root节点为根节点的树插入val并返回插入后的新树
        if (root==null) {
            return new TreeNode(val);
        }
        if (root.val < val) {
            root.right = insertIntoBST(root.right, val);
        }else{
            root.left = insertIntoBST(root.left, val);
        }
        return root; 
    }
}

首先, 明确这个函数返回的是插入后的新树, 给的是树的节点和要插入的值.

所以终止条件是, 如果树为空的时候, 直接返回一个val的新节点即可.

其他非终止条件情况是:

如果$root.val<val$, 则将val插入到root的右子树里面(可以用这个函数实现, 这也是为什么第一步确定函数是干什么的), 并且返回的是新的树, 所以才有了赋值
同上
最后插入了之后返回root.

转自知乎. 带你逐步分析递归算法的时间复杂度

来看一下这道面试题：求x的n次方

大家想一下这么简单的一道题目代码应该如何写。

最直观的方式应该就是，一个for循环求出结果，代码如下

int function1(int x, int n) {
    int result = 1;  // 注意 任何数的0次方等于1
    for (int i = 0; i < n; i++) {
        result = result * x;
    }
    return result;
}

时间复杂度为O(n)

此时面试官会说，有没有效率更好的算法呢。

如果同学们此时没有思路，建议不要说：我不会，我不知道。可以和面试官探讨一下，问：可不可以给点提示。

面试官一般会提示：考虑一下递归算法

有的同学就写出了如下这样的一个递归的算法，使用递归解决了这个问题

int function2(int x, int n) {
    if (n == 0) {
        return 1; // return 1 同样是因为0次方是等于1的
    }
    return function2(x, n - 1) * x;
}

面试官问：那么这份代码的时间复杂度是多少？

有的同学可能一看到递归就想到了logn，其实并不是这样

递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归中的操作次数

递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间。对于单线程来说，递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数，因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。

那我们再来看代码，我们递归了几次呢。

每次n-1，递归了n次时间复杂度是O(n)，每次进行了一个乘法操作，乘法操作的时间复杂度一个常数项O(1)

所以这份代码的时间复杂度是 n * 1 = O(n)

这个时间复杂度可能就没有达到面试官的预期。

于是同学又写出了这样的一个递归的算法的代码如下，来求 x的n次方

int function3(int x, int n) {
    if (n == 0) {
        return 1;
    }
    if (n % 2 == 1) {
        return function3(x, n/2) * function3(x, n/2)*x;
    }
    return function3(x, n/2) * function3(x, n/2);
}

面试官看到后微微一笑，问这份代码的时间复杂度又是多少呢？

我们来分析一下

首先看递归了多少次呢，可以把递归的次数抽象出一颗满二叉树。

我们刚刚写的这个算法，可以用一颗满二叉树来表示（为了方便表示我选择n为偶数），如图：

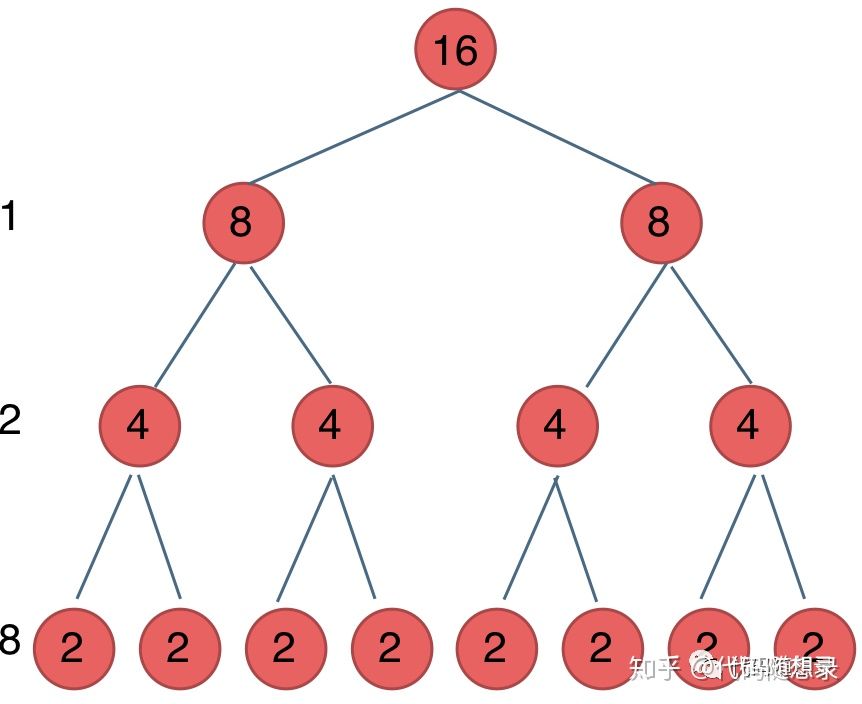
当前这颗二叉树就是求x的n次方，n为16的情况

n为16的时候我们进行了多少次乘法运算呢

这棵树上每一个节点就代表着一次递归并进行了一次相乘操作

所以进行了多少次递归的话，就是看这棵树上有多少个节点。

熟悉二叉树的同学应该知道如何求满二叉树节点数量

这颗满二叉树的节点数量就是2^3 + 2^2 + 2^1 + 2^0 = 15

有同学就会发现这其实是等比数列的求和公式，如果不理解的同学可以直接记下来这个结论。

这个结论在二叉树相关的面试题里也经常出现。

这么如果是求x的n次方，这个递归树有多少个节点呢，如下图所示

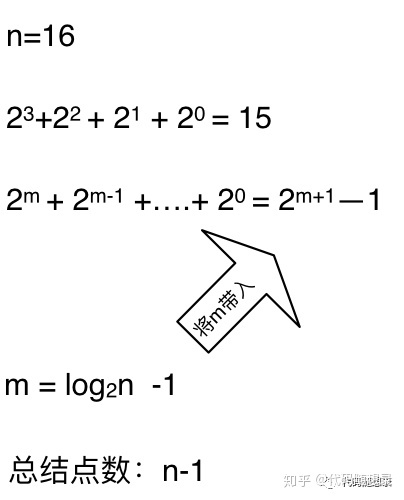
时间复杂度忽略掉常数项-1之后，我们发现这个递归算法的时间复杂度依然是O(n)。

此时面试官就会问，貌似这个递归的算法依然还是O(n)啊，很明显没有达到面试官的预期

那么在思考一下 O(logn)的递归算法应该怎么写

这里在提示一下上面刚刚给出的那份递归算法的代码，是不是有哪里比较冗余呢。

来看这份优化后的递归算法代码

int function4(int x, int n) {
    if (n == 0) {
        return 1;
    }
    int t = function4(x, n/2);// 这里相对于function3，是把这个递归操作抽取出来
    if (n % 2 == 1) {
        return t*t*x;
    }
    return t*t;
}

那我们看一下时间复杂度是多少

依然还是看他递归了多少次

我们可以看到这里仅仅有一个递归调用，且每次都是 n/2

所以这里我们一共调用了 log以2为底n的对数次

每次递归了做都是一次乘法操作，这也是一个常数项的操作，

所以说这个递归算法的时间复杂度才是真正的O(logn)。

其他

comparator

Returns:

a negative integer, zero, or a positive integer as the first argument is less than, equal to, or greater than the second.

(a, b) {return a- b } 1 2

(a, b) {return b-a} 1 2 ->2 1

记1, 2, 3, 4为顺序, 若顺序, 则a-b
若要逆序,则b-a

int a和int b的逆序怎么写

双端队列

Collections.reverse相关操作

Arrays.copyOfRange操作

欢迎在评论区中进行批评指正，转载请注明来源，如涉及侵权，请联系作者删除。