$$
\begin{aligned}
P\left(w_{1: n}\right) &=P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) P\left(w_{3} \mid w_{1: 2}\right) \ldots P\left(w_{n} \mid w_{1: n-1}\right) \
&=\prod_{k=1}^{n} P\left(w_{k} \mid w_{1: k-1}\right)
\end{aligned}
$$

这个1:k-1是序列的前缀,n-gram模型可以计算给定历史后的单词的概率,近似地用几个单词来代替历史.bigram模型将P(w_n|w_(1:n-1))用P(w_n|w_(n-1))来代替.也就是利用如下公式近似计算

$$
P(w_n|w_{1:n−1}) ≈ P(w_n|w_{n−1})
$$
基于Markov假设,一个单词出现的概率仅取决于前面出现的单词,所以计算条件概率可以用n-gram近似计算:
$$
P(w_n|w_{1:n−1}) ≈ P(w_n|w_{n−N+1:n−1}) = \frac{C(w_{n−N+1:n−1} w_n)} {C(wn−N+1:n−1)}
$$
这样的话就统计词频就可以了.

语料库的概率为0.0004,这并不意味着chinese在任何一个文本库中出现的概率为.0004,但是可以说明在一百万个单词的语料库中,它的概率为0.0004.在3.4节中本文提出了一个更好的概率估计方法.(文章中接下来基于一个语料库和bigram统计了词频).

在足够多的预料,我们更多使用4-gram或者5-gram,并且在句子开头增加填充字符用于计算第一个单词的概率.求解联和概率相乘导致数值下溢的问题,使用对数形式的概率来表示概模型的概率,这样乘法会转化为加法,在需要概率结果的时候,可以取e.

运行大的NLP任务作外部评估太昂贵了,所以可以使用一个内部评估方法.为了避免对测试集有针对性的调优,我们将这个测试集叫做devset用于调优,然后再用一个真正看不见的测试集来评测.测试几个不同的n-gram模型的方法是将数据集分为训练集和测试集,内部评估方法就是看哪个方法在经过在训练集上计算出的概率在测试集预测正确的准确率更高.我们想尽可能地想要足够大地训练集以学习到充足的特征,但是我们也想要尽可能大地训练集来评测.一般而言,我们8/1/1来划分训trainset, devset, testset.注意内在性能的提升并不保证在外部测试比如机器翻译等一定由提升.

如果测试数据出现在训练集中,会导致准确率偏高,并且导致巨大地不确定,这个不确定性我们称之为”困惑度”,公式如下:
$$
\begin{aligned}
\operatorname{PP}(W) &=P\left(w_{1} w_{2} \ldots w_{N}\right)^{-\frac{1}{N}} \
&=\sqrt[N]{\frac{1}{P\left(w_{1} w_{2} \ldots w_{N}\right)}}
\end{aligned}
$$
在概率计算中我们需要包含<s>和在计算单词总数的时候我们需要包含,但不用.perplexity作为语言的权重平均分支因子,语言的分支因子是单词可能跟着的单词的数目.在计算perplexities时，n-gram模型P必须在没有任何测试集知识或任何测试集词汇的先验知识的情况下构造.在比较两个语言模型时必须在同一个词汇表上.

n-gram有几个缺点如下:

我们是基于训练语料库训练的,但是有些句子可能会出现的并没有出现在语料库中,这部分zero count的概率我们没有计算出.

另外有些单词为为Unkown Words.

这些Zeros从两种原因上是一个问题:

意味着我们低估了也许会出现的短语的概率.

在测试集中出现的概率为0,那就不能计算perplexity,因为perplexity是逆概率,分母不能为0.

而处理Unkown Words的方法是增加一个来指代,计数有两种方法.

第一种方法:

提前给定单词表.

在文本归一化过程中将单词表以外的单词都视为.

像正常单词一样评估的概率.

第二种方法:

没有给定单词表,统计单词的频度,将低于某一频度的单词统一视为.

像正常单词一样评估的概率.

所以,有Zero和这种情况,我们需要分配一些概率给它们,这种方法叫做smoothing或者discounting.

Laplace smoothing将bigram对单词的计数在计算成概率之前+1,这样0次计数就变成了1次计数.它对于n-gram模型的表现不太好,但是是我们理解其它smoothing方法的一个baseline,另外Laplace smoothing在text classigication任务中是一个有用的算法,这个算法也叫做add-one smoothing.

add-k smoothing将上面的1替换成k即可.

另一种平滑的思想是backoff和interpolation.backoff指的是在使用n-gram时,将n-gram由高到低看作n-gram hierarchy,当高层n-gram概率为0的时候,用低层n-gram的概率代替.interpolation是把几个不同的n-gram概率混杂在一起.

一种backoff方法叫做Katz backoff.我们需要将某些高维的N-grams的值减小为了将他们赋予那些高维n-gram为零用low gram代替的词,否则概率堆会变大,也就是总和大于1.所以我们需要一个函数α来分配概率堆给low order n-grams.这种backoff叫做Katz backoff.Katz backoff经常与叫做Good-Turing的平滑方法联用.

discount的方法将n-gram打多少折扣合适?Church and Gale用在一个22 million的语料库中4次的序列,看在另一个22 million的语料库中出现的次数.平均下来,前者为4次的话,后者为3.23次.Kneser-Ney discounting是通过更复杂的方法处理低阶n-gram，增强绝对discounting.

现在在预测下一个词出现的概率有另一个问题的出现.Kong比glasses有着更高的概率,但是glasses比Kong有着更广泛的分布,为了评估一个单词在新上下文出现的概率,Kneser-Ney提出了一个基于单词w已经出现在不同的上下文环境中的次数的概率P_CONTINUATION.最终形成了一个最终Interpolated Kneser-Ney:
$$
P_{\mathrm{KN}}\left(w_{i} \mid w_{i-1}\right)=\frac{\max \left(C\left(w_{i-1} w_{i}\right)-d, 0\right)}{C\left(w_{i-1}\right)}+\lambda\left(w_{i-1}\right) P_{\mathrm{CONTINUATION}}\left(w_{i}\right)
$$
后面还介绍了一种stupid backoff和困惑度所基于的信息熵的一些数学原理.

问题:

虽然说是预测下一个单词,但是在某些问题中,比如完型填空,是否可以使用两次n-gram(空前的句子为1次,空后的句子为1次)来综合考虑该位置上的单词概率?

Chapter 6 N-gram Language Models
向量语义与静态词嵌入——从tf-idf到GloVe

Speech and Language Processing

6.1 Lexical Semantics(词汇语义)
介绍了一些术语:

lemma(citation form):mouse有很多意思,这个mouse就是lemma.

wordfrom

synonym(propositional meaning): 同义.

principle of contrast: H2O和water虽然有相同的含义,但是不同的语言形式也蕴含着一些意义上的区别.

relatedness(association): 相关,cup和coffee不同义但相关.

semantic field: 相关的单词趋向于出现在相同的语义场.

topic model: 语义场与主题模型也紧密联系,就像LDA.

semantic frame: 语言框架,可以用来结构化表示相同类型的句子的信息.比如buyer buy what.

connotation: 含义,可以是emotion, sentiment, opinions和evaluation.

单词往往有三种维的情感意义:

valence 高兴程度

arousal 情感紧张程度

dominance 情感控制程度

6.2 Vector Semantics(向量语义)
vector semantics在NLP中是表示单词的一个基本方法,向量表示单词叫做embeddings(嵌入),经常用的方法是产生密集向量的word2vec,产生稀疏向量的PPMI比较少用.单词embedding来源于数学,意义是从一个空间映射到另一个空间.vector smeantic model可以无监督学习得到.

在本章我们介绍ti-idf模型(会产生长稀疏向量)和word2vec模型(会产生短密集向量)以及cosine(计算向量的相似性的一种常用方法).

6.3 Words and Vectors
向量或者分布模型通常基于co-occurence matrix,这个矩阵代表了单词们共同出现的经常程度,两种比较流行的矩阵式tem-document matrix和term-term matrix.

6.3.1 Vectors and documents
term-document matrix行轴为单词表中的单词,列为文章集的文章,每个item表示行单词在列文章中出现的次数.每个列向量可以用来表示该列的文章,列向量上的数字表示在该行单词维度上对于文章的刻画.同样的,行向量也可以用来表示单词.真实情况下,单词表的大小为上千大小,文档的数量也十分巨大(想象一下互联网上的文章).该矩阵最初被用来在文档信息检索任务中寻找相似的文档.

6.3.2 Words as vectors: document dimensions
单词也同时被表示成了向量(行向量),列向量相似文档相似,同样的,行向量相似,则单词也相似,因为他们趋向于出现在相似的文档.

6.3.3 Words as vectors: word dimentsions
把term-document的document代替为context就变为了term-term/context matrix(word-word matrix). context可以取4个单词范围,每个单元表示行单词在列上下文中出现的次数.这个矩阵大小为|V|*|V|,所以会有很多的单元为0.有一些算法可以存储并计算稀疏矩阵.

6.4 Cosine for measuring similarity
用点积(内积)可以刻画两个向量的相似程度,值越大越相似.但是我们并不关心具体的值的大小,我们只关心相似程度,所以需要normalize以下,normalize的方法就是内积除以向量大小
$$
\frac{\boldsymbol{a}\cdot \boldsymbol{b}}{\left| \boldsymbol{a} \right|\left| \boldsymbol{b} \right|}=\cos \theta
$$

6.5 TF-IDF: Weighing terms in the vector
单词出现的频率越高越好,说明信息量比较大,但是我们又不是很希望太高,就像the,it这种,出现的太高又无意义,所以如何平衡这中悖论呢?有if-idf和PPMI模型.

tf-idf模型计算依赖tf和idf两个公式.

tf公式由$ count(t,d) $转为$ log_{10}(count(t,d)+1) $.

idf公式为$ log_{10}(\frac {N} {df}) $

tf-idf的计算公式为:
$$
w_{t,d} = tf_{t,d} \times idf_t
$$

6.6 Pointwise Mutual Information (PMI)
PMI计算公式(假设他们互相独立,衡量两个事件同时出现的频率)

$$
PMI(w,c) = log_2{\frac {P(w,c)} {P(w)P(c)}}
$$

PMI可以为负值,但是意义不大,所以经常使用PPMI:

$$
PPMI(w,c) = max(log_2{\frac {P(w,c)} {P(w)P(c)}}, 0)
$$
PMI的问题是非常稀少的单词也有很高PMI值,改进PMI偏好低频词的方法有两种:

使用$ P_\alpha(C) $

利用拉普拉斯平滑,在计数PMI前给每个count加上0.1-3.

6.7 Applications of the tf-idf or PPMI vector models
可以通过将单词的向量加和求平均来表示文档,这个结果向量叫做document vector,它可以比较文档的相似性,应用到信息检索等任务.

6.8 Word2vec
word2vect生成的为短密集向量,向量元素为实数,可以为负数.

短密向量比长稀向量直觉上更好的原因是:

前者比后者学习更少的权重

前者更小的参数空间更有可能对泛化和防止过拟合有帮助.

前者比后者更容易计算出两个单词的同义性,比如car和automobile在稀疏向量时比较遥远和不相关.

在本章介绍skip-gram with nagative sampling(SGNS), skip-gram是一个叫做word2vec算法软件包中的一个算法,有时候也指代word2vec.

Word2vector训练一个二元分类器,将分类器的权重作为单词嵌入的向量而非关注分类任务.这个方法的创新之处是将w是否出现在apricot附近作为标签,不需要我们手工添加标签,这种方法叫做自监督.

wrord2vec从两点来看是一个神经网络模型:

word2vec是二分类任务.

word2vec将复杂的结构简化逻辑回归分类器.

skip-gram思想的四步骤:

把目标单词和相邻的上下看作正样例.

在词汇表中随机选择单词作为负样例.

用逻辑回归模型训练两种cases的分类器.

用训练的权重作为嵌入向量.

6.8.1 The classifier
正样例的概率记为$ P(+|w,c) $,单词c不是w的上下文概率记为$ P(-|w,c) = 1- P(+|w,c) $,这个概率怎么算?

skip-model应该基于嵌入向量的相似性:一个单词如果与上下文相似,则可以用点击来衡量,也就是$ Similarity(w,c) ≈ c ·w $,但这个不是概率,所以可以用logistic或者sigmoid函数来将它变为概率,最后的概率计算公式为:
$$
P(+|w,c) = \sigma(\boldsymbol{c} \cdot \boldsymbol {w})=\frac {1}{1+exp(-\boldsymbol{c} \cdot \boldsymbol {w})}
$$
上式只是计算了上下文中一个单词与w的概率,而上下文是多个词,所以上下文与单词w出现的概率就是相乘取对数.
$$
\log P\left(+\mid w, c_{1: L}\right)=\sum_{i=1}^{L} \log \sigma\left(\mathbf{c}_{\mathbf{i}} \cdot \mathbf{w}\right)
$$
我们需要学习的参数是两个矩阵$ W $和$C$.

6.8.2 Learning skip-gram embeddings
skip-gram首先为每个 N 词汇单词分配一个随机嵌入，然后继续迭移每个单词 w 的嵌入，使其更像文本中上下文的单词的嵌入，而不像非上下文单词的嵌入.通常负样例的个数是正样例个数的k倍,k=2.负样例单词的选择依赖于他们的unigram的频率值$P_\alpha(w)$,$\alpha$通常取$\frac {3} {4}$,这样可以给出现次数少的词更高的概率,而出现次数多的单词赶驴下降的也不是很多.公式为:
$$
P_\alpha(w)=\frac {count(w)^\alpha} {\sum_{w’}count(w’)^\alpha}
$$
学习算法的目标是调整嵌入向量

最大化正样例的相似性

最小化负样例的相似性

损失函数为:
$$
\begin{aligned}
L_{C E} &=-\log \left[P\left(+\mid w, c_{p o s}\right) \prod_{i=1}^{k} P\left(-\mid w, c_{n e g_{i}}\right)\right] \
&=-\left[\log P\left(+\mid w, c_{p o s}\right)+\sum_{i=1}^{k} \log P\left(-\mid w, c_{n e g_{i}}\right)\right] \
&=-\left[\log P\left(+\mid w, c_{p o s}\right)+\sum_{i=1}^{k} \log \left(1-P\left(+\mid w, c_{n e g_{i}}\right)\right)\right] \
&=-\left[\log \sigma\left(c_{p o s} \cdot w\right)+\sum_{i=1}^{k} \log \sigma\left(-c_{n e g_{i}} \cdot w\right)\right]
\end{aligned}
$$
采用梯度下降法得到梯度:
$$
\begin{aligned}
&\frac{\partial L_{C E}}{\partial c_{p o s}}=\left[\sigma\left(\mathbf{c}{p o s} \cdot \mathbf{w}\right)-1\right] \mathbf{w} \
&\frac{\partial L{C E}}{\partial c_{n e g}}=\left[\sigma\left(\mathbf{c}{n e g} \cdot \mathbf{w}\right)\right] \mathbf{w} \
&\frac{\partial L{C E}}{\partial w}=\left[\sigma\left(\mathbf{c}{p o s} \cdot \mathbf{w}\right)-1\right] \mathbf{c}{p o s}+\sum_{i=1}^{k}\left[\sigma\left(\mathbf{c}{\mathbf{n} e g{i}} \cdot \mathbf{w}\right)\right] \mathbf{c}{n e g{i}}
\end{aligned}
$$
因此,参数更新公式为:
$$
\begin{aligned}
\mathbf{c}{p o s}^{t+1} &=\mathbf{c}{\text {pos }}^{t}-\eta\left[\sigma\left(\mathbf{c}{\text {pos }}^{t} \cdot \mathbf{w}^{t}\right)-1\right] \mathbf{w}^{t} \
\mathbf{c}{n e g}^{t+1} &=\mathbf{c}{n e g}^{t}-\eta\left[\sigma\left(\mathbf{c}{n e g}^{t} \cdot \mathbf{w}^{t}\right)\right] \mathbf{w}^{t} \
\mathbf{w}^{t+1} &=\mathbf{w}^{t}-\eta\left[\left[\sigma\left(\mathbf{c}{p o s} \cdot \mathbf{w}^{t}\right)-1\right] \mathbf{c}{p o s}+\sum_{i=1}^{k}\left[\sigma\left(\mathbf{c}{\mathrm{n} e g{i}} \cdot \mathbf{w}^{t}\right)\right] \mathbf{c}{n e g{i}}\right]
\end{aligned}
$$
skip-gram学习到两个参数嵌入在两个矩阵中,最终单词的表示可以为这两个参数嵌入的加和.

6.8.3 Other kinds of static embeddings
其它嵌入方法还有fastext,GloVe等.

6.9 Visualizing Embeddings ATLANTA
介绍了三种可视化向量的方法:

最简单的方式是将相似的单词聚类.

另一种方法是利用聚类方法将向量展示为树状结构.

最常用的方法是将高维向量降维为2维向量.

6.10 Semantic properties of embeddings
这节对于前面embeddings的semantic properties做一个总结.

context窗口的选择,小则考虑两个单词的同义性,大则考虑两个单词同主题的相关性.

考虑单词相似性或者联系性,first-order co-occurrence(systangmatic association)指的是类似与wrote与poem/book的这种关系.second-orde co-occurrence(paradigmatic association)指的是类似于wrote和said/remaked的这种关系.

parallelogram model可以进行类比,比如给出apple-tree和grape来预测第四个词,而这四个词的嵌入往往是一个平行四边形,另一个词会被parallelogram model预测为vine,但是这个模型在一些情况下也不适用.

6.10.1 Embeddings and Historical Semantics
词嵌入也可以用来学习单词的语义是如何随着事件变化的(根据相同的单词在向量空间随着事件推移的变化).

6.11 Bias and Embeddings
词嵌入的学习也许会蕴藏一些成见.

6.12 Evaluating Vector Models
评估向量模型最好的办法就是应用到外部任务中看性能是否提升,但内在评估也同样重要,这节介绍了几个数据集用来评价vector model的性能.有的数据集只有单词,有的数据集还有上下文.

问题
PMI为负的情况下为什么意义不大呢,为什么会在超大语料库下负的PMI才有用?b

Chapter 7 Neural Networks and Nuural Language Models
参考翻译: https://www.kancloud.cn/drxgz/slp20201230/2316550

7.1 Units
介绍了神经网络种一个基本的计算单元的一些概念:

bias term: 偏置

dot product: 计算单元可以写成点积形式.

activation: 激活函数,将点积结果再进行一次非线性变换.

sigmoid: sigmoid函数就是s型函数,常见的形式为:
$$
\sigma(z) = \frac {1} {1+e^{-z}}
$$

tanh: 实际使用中并不使用sigmoid函数,而是使用tanh函数:
$$
\sigma(z) = \frac {e^z-e^{-z}} {e^z + e^{-z}}
$$

ReLU: 最简单的激活函数(但也许不是最常用的)函数是ReLU函数:
$$
y = max(z,0)
$$

不同的激活函数有不同的特点,tanh函数的微分很平滑并且可以将离群值朝着均值方向映射,修正函数(ReLU)的特点是非常接近线性函数,Sigmoid和tanh函数的值非常 saturated(非常接近于1的地方导数为0),容易在反向传播过程种造成梯度消失,而ReLU函数没有这样的问题.

7.2 The XOR problem
感知机可以解决与和或问题但是不能解决异或分类问题,解决方法就是用神经网络,在中间加一层隐藏层,利用隐藏层将输入转化为另一种形式再作为输出层的输入进行分类.并在神经网络必须用非线性函数作激活,因为用线性函数作激活总能简化为一个线性分类器.

7.3 Feedforward Neural Networks
最简单的神经网络模型叫做前馈神经网络,有时候也被称之为多层感知机,神经网络中最重要的是就是隐藏层.在标准结构中,每层都是全连接的(意思是下一层的每个节点的输入都是上一层的所有阶段的输出).

假设隐藏层由 $m$ 个,输入有 $n$ 个,则 $W$ 矩阵大小为 $m*n$ 大小,第 $i$ 个输入节点对应第 $j$ 个隐藏层的权重为 $w_{[j,i]}$ ,也就是说 $w_{[i,j]}$对应第 $j$ 个输入节点到第 $i$ 个输出节点的权重.

隐藏层的输出如下:
$$
\boldsymbol{h}=\sigma(\boldsymbol{Wx} + \boldsymbol{b})
$$
可以把 $\boldsymbol{x}$ 的维数增加一维,令 $x_0=1$,$\boldsymbol {W}$对应位置也增加一维赋值为 $b$, 就可以直接写成向量点积的形式了.

输出层的输出如下(这里省略掉偏置用于简化式子):
$$
\boldsymbol {z} = \boldsymbol {Uh}
$$
在一般的神经网络中,输出的是实数,但是我们在作分类任务时,需要的是概率,所以要把实数归一化为概率,这里有一个函数是我们在第5章提到softmax,即最后再使用sigmoid函数:
$$
\boldsymbol {y} = softmax(z)
$$
输入层,隐藏层,输出层这样的一个网络是2层网络,我们一般不把输入看作一层但把输出层看作一层,所以逻辑回归模型是一个一层的神经网络.

7.3.1 More details on feedforward networks
这节讲了统一的符号表示,然后表示了一些多层网络的计算,比如:

$\boldsymbol {W}^{[1]}$表示第一层隐藏层的权重,方框里的数字表示第几层,输入层看作第0层.

$\boldsymbol {b} ^{[1]}$表示第一层的偏置.

$n_j$表示第j层的节点

$g(\cdot)$表示激活函数

$\boldsymbol {z}^{[1]}$表示未经激活的点积+偏置的输出

$\boldsymbol {a}^{[1]}$表示激活激活的输出

$\hat{y}$表示输出层的输出

$y$表示真正的输出

所以,算法表示如下:

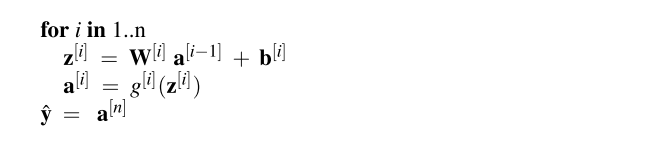
7.4 Feedforward networks for NLP: Classification
利用前馈神经网络可以进行自然语言处理任务文本情感分类,输入元素可以是标量特征,比如特征向量中第一个元素 $x_1$为文本中的单词再单词表中出现的总次数,$x_2$为文本中属于积极词性的单词的个数,$x_3$为如果有”no”在单词表中为1等等(也就是自己手动构建特征,而在学习的过程学习权重),输出是两个节点(或者三个节点(积极,消极,中性).

更多的NLP任务不用手动构建特征,而是使用单词的嵌入的串联,这叫做预训练,网络模型如下:
$$
\begin{aligned}
\mathbf{x} &=\left[\mathbf{e}{w 1} ; \mathbf{e}{w 2} ; \mathbf{e}{w 3} ; \cdots ; \mathbf{e}{w n}\right] \
\mathbf{h} &=\sigma(\mathbf{W} \mathbf{x}+\mathbf{b}) \
\mathbf{z} &=\mathbf{U h} \
\mathbf{y} &=\operatorname{softmax}(\mathbf{z})
\end{aligned}
$$

7.5 Feedforward Neural Language Modeling
另一个前馈神经网络模型的的应用是语言模型:从前面的单词上下文预测将要出来的单词.相比于n-gram模型,神经网络模型可以处理更长的历史, 在处理相似单词的上下文时表现更好, 并且对于单词的预测更准确. 但是, 神经网络更复杂, 训练地慢, 更低的可解释性, 所以在一些(较小)的任务中n-gram模型依然是很好的工具.神经网络模型表示前面的上下文用嵌入而非n-gram模型中的单词的特征, 使用嵌入允许神经网络模型对没有出现的单词泛化的很好.

7.5.1 Forward inference in the neural language model
预测下个单词的神经网络模型如下:

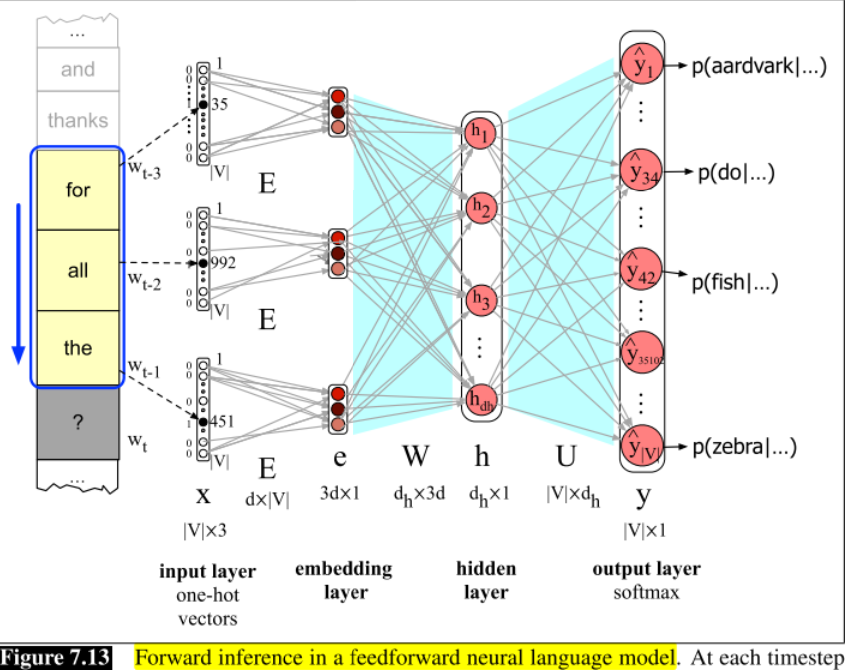
7.6 Training Neural Nets
误差损失函数是
$$
L_{C E}(\hat{y}, y)=-\log \frac{\exp \left(\mathbf{z}{i}\right)}{\sum{j=1}^{K} \exp \left(\mathbf{z}_{j}\right)} \quad \text { (where } i \text { is the correct class )}
$$
用偏导计算梯度(对于一层网络和sigmoid输出的逻辑回归).

当遇到更多层网络时,利用误差反向传播算法(其要点就是链式法则):

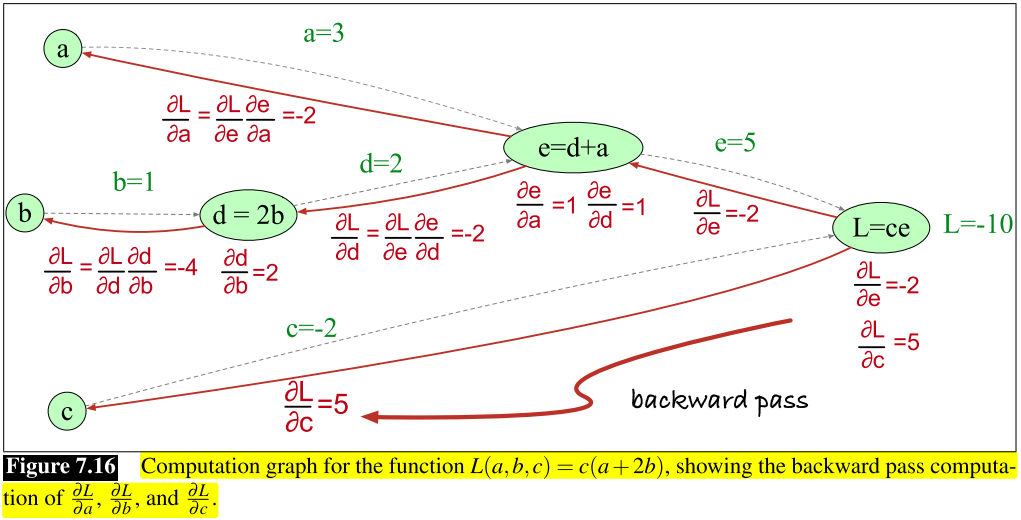
神经网络的优化是一个非凸优化问题, 对于此问题有很多的方法提出.

用于防止过拟合的方法之一是dropout, 也就是把某些神经网络的节点人为的去掉.

有一些超参数(不是由机器学习学到的参数)的选择也是非常重要,比如学习率,批大小.

7.7 Training the neural language model
一般的神经网络语言模型的参数$\theta = \boldsymbol {E,W,U,b}$,本节显示如何训练一个一般的神经网络语言模型.

对于一些语言模型,冻结某些参数也很有用, 比如$E$, 也就是在训练过程中不改变它, 但经常也去更新$E$,神经网络的训练过程如下:

损失函数用交叉熵:
$$
L_{CE}(\hat y,y)=-\log(\hat{y_i}) \text{(where i is the correct class)}
$$
对于语言模型,$\hat{y_i}$是模型赋值给下一个正确的单词的概率:
$$
L_{CE}=\left[-\log p\left(w_{t} \mid w_{t-1}, \ldots, w_{t-n+1}\right)\right]
$$

参数更新公式如下:
$$
\theta^{s+1}=\theta^{s}-\eta \frac{\partial\left[-\log p\left(w_{t} \mid w_{t-1}, \ldots, w_{t-n+1}\right)\right]}{\partial \theta}
$$

Question:
可否将神经元unit先”组合”成一个大的”神经元”再进行下层的连接呢?

ChapSequence Labeling for Parts of Speech and Named Entites
8.1 (Mostly) English Word Classes
词语分为两大类:

封闭类:成员关系相对固定的类,比如介词,他们通常是虚词.

开放类:通常是名次,动词,形容词和副词,以及较小的感叹词.

还有一种常见的分类是:名词,动词,形容词,副词,感叹词,介词,小品词,限定词,连词,代词.

8.2 Part-of-Speech Tagging
part-of-speech tagging(词类标记)是为文本中的每个单词分配词类的过程, 给定输入单词和标签集,输出是输入单词对应的标签序列.词类标记是一个消除歧义的任务, 词类标记算法的准确性的基线和SOTA和人类最高水平(97%)仅差5%.

8.3 Named Entities and Named Entity Tagging
命名实体是可以用专用名称表示的任何东西:人,位置或者组织.命名实体识别的任务是查找构成转悠名称的文本范围并标记实体的类型.最常见的是四个实体标签:PER,LOC, ORG, GPE. 命名实体标记是许多自然语言处理任务中有用的第一步.

词类标记与命名实体识别的不同之处在于词类标注不会因为每个单词获得一个标记残生分段问题.常见的序列标记方法有BIO和IO.

8.4 HMM Part-of-Speech Tagging
本节介绍第一个序列标记算法-隐马尔可夫木星,并且展示如何将其应用到词类标记.

8.4.1 Markov Chains
Markov chain是一个模型, 它告诉我们有关随即便来给你,状态序列的概率的信息, 每个状态都可以从集合中取某个值.马尔科夫链建设在马尔可夫假设之上：
$$
P（q_i=a|q_1…q_{i-1})=P(q_i=a|q_{i-1})
$$

8.4.2 The Hidden Markov Model
有些情况我们感兴趣的事件是隐藏的，我们不会之间观察他们。比如文本中观察到词类标记，这些标记为隐藏标记。隐马尔可夫模型允许我门讨论观察到的事件和隐藏事件，我们将他们视为概率模型中的因果关系，一个HMM由以下组件指定：

异界隐马尔可夫模型实例化两个简化假设：

特定状态的概率仅取决于之前的状态。

输出观测值$O_i$的概率仅取决于产生的观测值$q_i$的状态，而不取决于任何其他状态或任何其他观测值。

8.4.3 The components of an HMM tagger
HMM有两个成分：A和B的概率。

A矩阵包含标记转换概率$P(t_i|t{i-1})$，表示给定先前标记的情况下标记出现的概率。

B发射概率$P(w_i|t_i)$表示在给定标签的条件下，它与给定单词相关联的概率。发射概率的MLE为：
$$
P(w_i|t_i) = \frac {C(t_i,w_i)} {C(t_i)}
$$
HMM词类标记器中的三个状态的HMM的A转移概率和B观察概率如图：

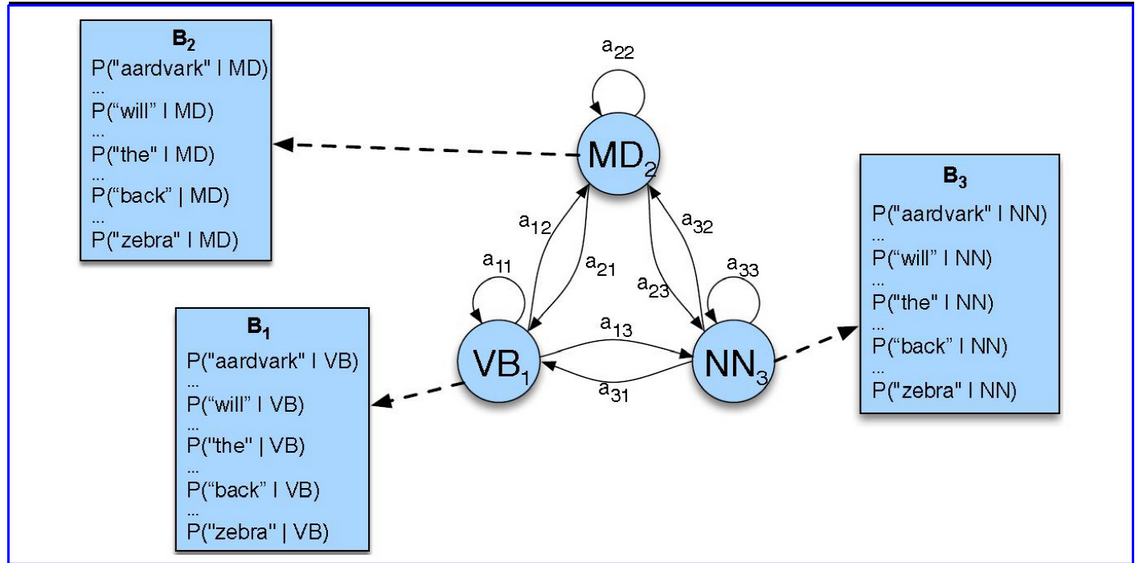
8.4.4 HMM tagging as decoding
HMM确定与观察序列相对应的隐藏变量序列的任务称为解码，对于词类标记，HMM的解码目标是在给定单词观察序列的情况下，选择最有可能的标记序列，最后得到的公式如下：

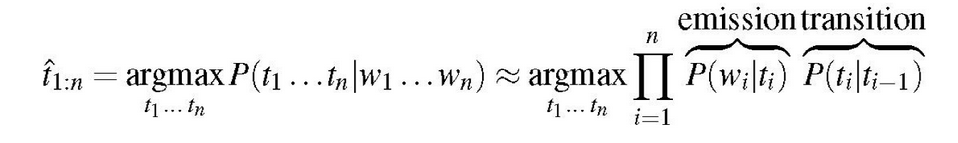
8.4.5 The Viterbi Algorithm
HMM的解码算法是维特比算法。

8.4.6 Working through an example
展示了一个例子。

8.5 Conditional Random Fields (CRFs)
HMM有一个缺点是需要大量的增强来实现较高的精度，HMM生成的模型很难以干净的方式直接向模型中添加任意特征，但是有一个基于对数线性模型的区分式序列模型条件随机场（CRF）可以做到。本节我们介绍线性链CRF，最常用于语言处理的CRF版本以及与HMM紧密匹配的CRF版本。

给定输入单词序列并想计算一个输出标记序列，HMM依赖于贝叶斯规则和似然度，而CRF则直接计算后验P（Y|X）。但是CRF不会在每个时间步为每个标签计算概率，而是通过在每个时间步计算一组相关特征的对数线性函数，并将这些局部特征汇总并归一化以产生整个序列的全局概率。

8.5.1 Features in a CRF POS Tagger
CRF不会为每个局部特征fk学习权重，相反首先将整个句子中每个局部特征的值相加，以创建每个全局特征，然后将这些全局特征乘以权重，因此为了训练和推理，即使每个句子的长度不同，也有K个权重的K个特征的固定集合。

8.5.2 Features for CRF Named Entity Recognizers
地名词典是一个对位置特别有用的特征，是地名词典名称的列表，可以将其实现为二进制特征，以只是短语出现在列表中。此外展示了实体符号的非零特征值和一个例子。

8.5.3 Inference and Training for CRFs
CRF中的学习依赖于我们为逻辑回归提供的相同的监督学习算法。给定一系列观察值、特征函数和相应的输出，我们使用随机梯度下降法训练权重，以最大程度地提高训练语料库的对数似然度。线性链CRF 的局部性质意味着可以使用CRF版本的前向后向算法来有效地计算必要的导数，与逻辑回归一样，L1或L2正则化也很重要。

8.6 Evaluation of Named Entity Recognition
命名实体识别通过召回率，精度和F1度量进行评估。

8.7 Further Details
总结数据：介绍了一些数据集。

总结模型：下面几节：

8.7.1 Bidirectionality
CRF和HMM架构的一个问题是，这些模型只能从左到右运行。尽管维特比算法仍然允许当前决策受到将来决策的间接影响，但如果有关单词$W_i$的决策可以直接使用有关未来标记$t_{i+1},t_{1+2}$的信息，则将提供更大的帮助。

另外可以通过使用多次遍历将任何序列模型转换为双向模型。

8.7.2 Rule-based Methods
还可以使用基于规则的方法：

1 .首先，使用高精度规则来标记明确提及的实体。
2 .其次，搜索与之前检测到的名称匹配的子字符串。
3 .再次，使用特定于应用程序的名称列表来查找可能特定领域的提及。
4 .最后，应用有监督的序列标签技术，使用来自之前的阶段的标记作为附加特征。

8.7.3 POS Tagging for Morphologically Rich Languages
对于其它一些形态丰富的语言必须增强标记算法。

Chapter 9
传统的基于窗口的语言模型通过接收固定大小的符号窗口作为输入来运行, 最终输出跨越输入的一系列预测. 但是这种通用的方法存在一些问题, 比如N-gram方法限制了可以从中提取的上下文, 上下文窗口外的任何内容不会影响所做出的预测. 但是这里就有问题了,因为很多任务都需要访问可能与处理发生地点任意距离的信息.其次是窗口的使用使得网络很难学习像成分等现象引起的系统模式. 本章就是为了解决这两个问题所产生的两个深度学习框架RNN和Transformer.两种方法都允许在不适用任何固定大小的窗口的情况下处理可变长度的输入, 并且利用到语言的时间性质.

之前的n-gram和前馈神经网络都建立在马尔可夫假设之上:
$$
P(w_n|w_{1:-n-1}) \approx P(w_n|w_{(n-N+1):(n+1)})
$$
这个假设表明预测一个大小为N的固定的先前上下文此前发生的任何输入与结果都没有关系, 而本章的语言模型会放宽这个假设, 允许模型使用更大的上下文.

RNN
最基本的RNN的结构是这样的:

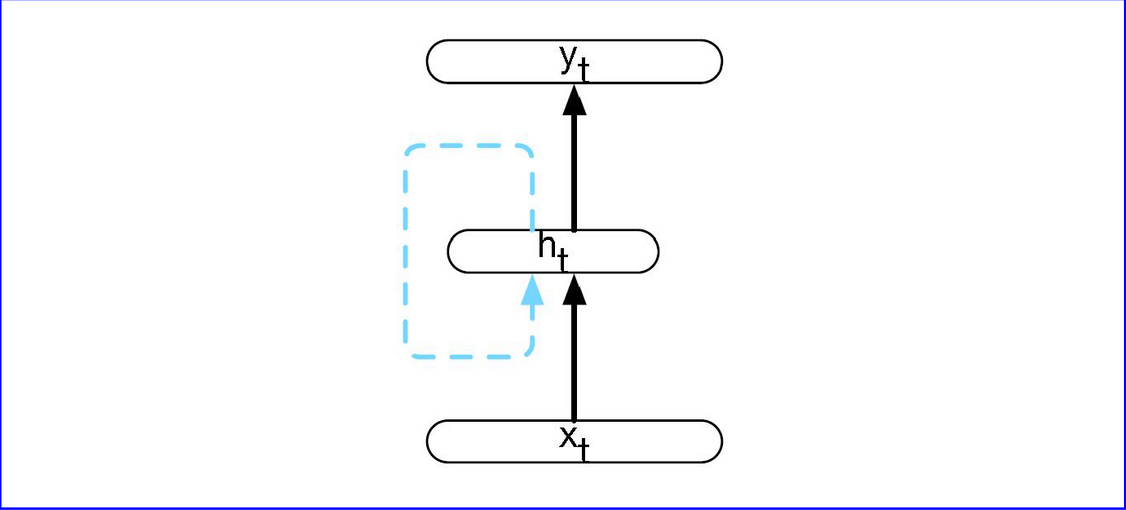
与前馈神经网络不同的是隐层的输出会用作下一层隐层的输入, 也就是”反馈”,

RNN的前向计算公式:
$$
h_t = g(Uh_{t-1}+Wx_t)
$$

$$
y_t = f(Vh_t)
$$

而将RNN的循环网络进行展开为前馈计算图则可以消除显示的循环, 从而可以直接训练网络的权重:

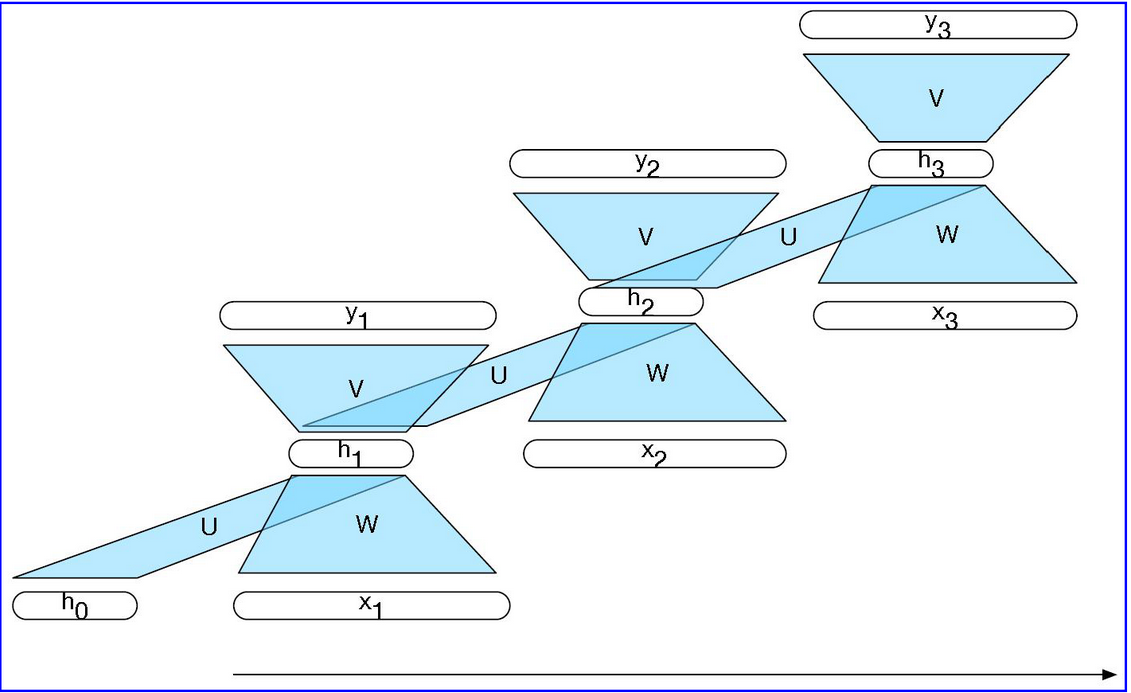
RNN可以用作语言模型,序列标签以及序列分类.

在基础的RNN上有两个更常见的网络架构: 堆叠RNNs和双向RNNs

堆叠RNNs由多个网络组成, 其中的一层输出充当下一层的输入, 如图:

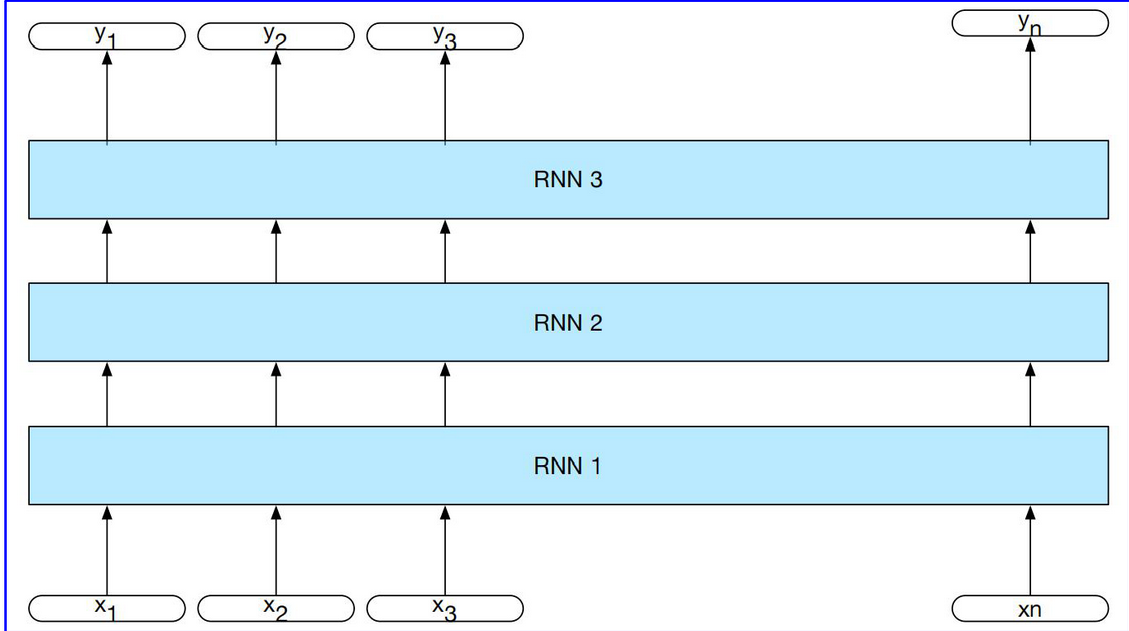
双向RNNs是将可以访问整个输入序列的右侧的上下文也作捕获作为输入, 这时候将传统的左侧上下文和右侧撒谎给你下问进行一个组合产生新的输入, 这就是双向RNNs的思想:

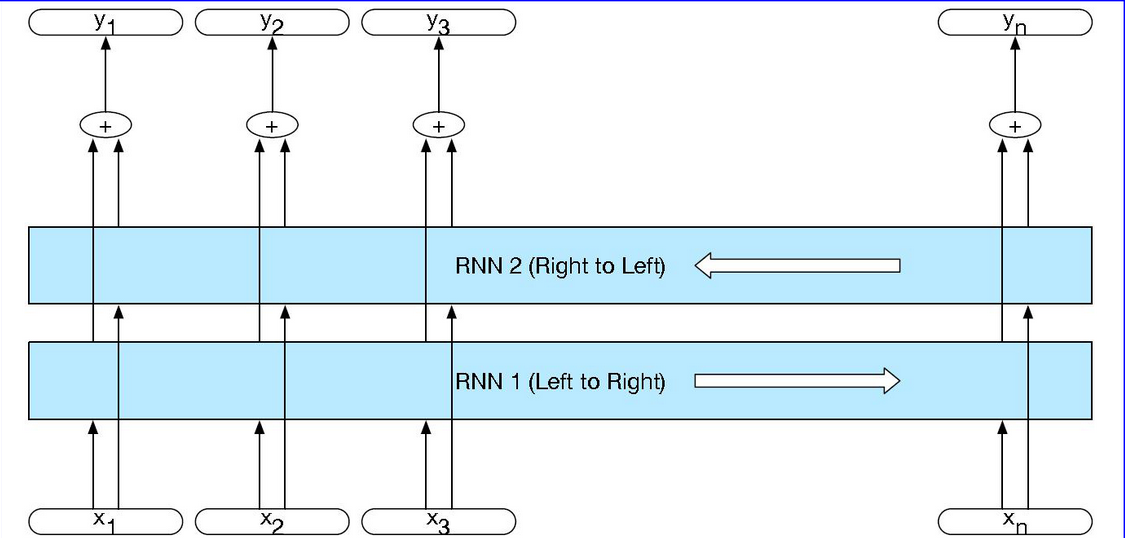
LSTM就是基于RNN的神经网络模型, 它将上下文管理问题分为两个子问题, 从上下文中删除不再需要的嘻嘻你系, 以及添加以后进行决策可能需要的信息.LSTM利用一个gate进行信息流的控制, 单个LSTM单元的计算图如下所示:

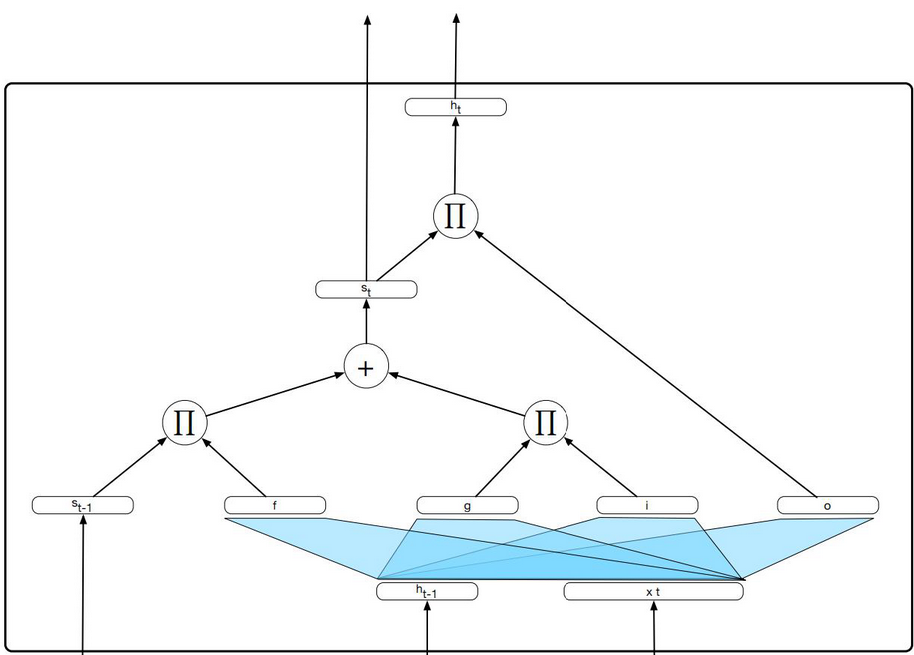
其中,
$$
f_t = \sigma(U_fh_{t-1}+W_{f}x_t)
\
k_t = c_{t-1}⊙f_t
\
g_t = tanh(U_gh_{t-1}+W_gx_t)
\
i_t = \sigma(U_ih_{t-1}+W_tx_t)
\
j_t = g_t⊙i_t
\
c_t = j_t+k_t
$$
GRU的花就是简化了$c_t$

Transformer
LSTM虽然可以环节远程信息丢失的问题, 但还是存在一些潜在的问题, 通过扩展的一些列循环连接向前传递信息会导致相关信息的丢失和训练上的困难, 并且并行计算也被限制了, 所以就产生了Transformer, 一种序列的处理方法可以消除循环连接以方便并行化.

Transfomer的关键创新是使用self-attention层, 自注意力机制可以使得网络从任意大的上下文中提取和使用信息, 而无需像RNN那样通过中间的循环传递信息, 它在处理输入的每个item时候, 可以访问所有的输入, 但是无法访问有关当前输入之外的输入信息, 另外每个项的执行计算独立于其他计算, 前者确保我们可以用这种方法创建语言模型, 后者可以确保我们可以并行化前向计算和训练.

自注意力机制如下:

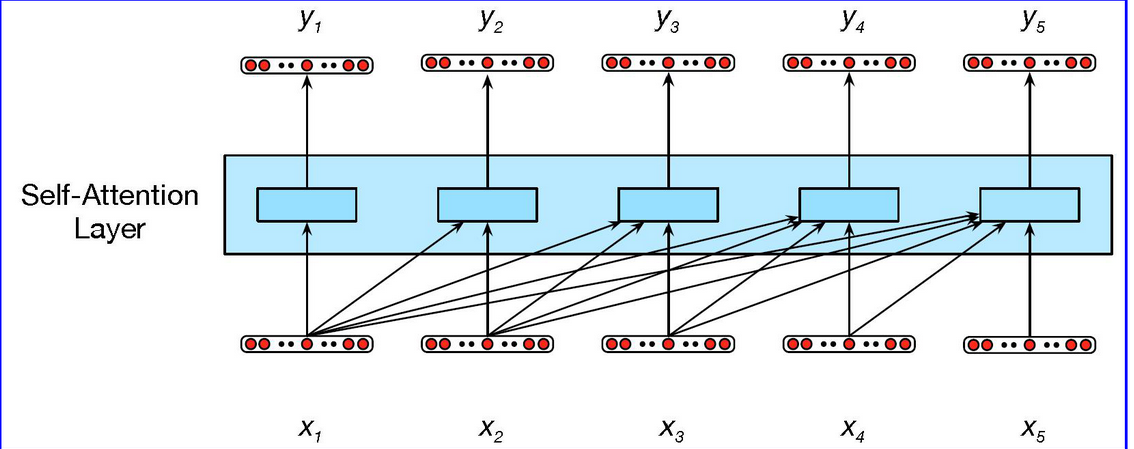
每个输入嵌入在注意力过程中扮演不同的角色:

Q: 和其他所有先前输入比较时, 扮演当前注意力的焦点角色

K: 与当前注意力焦点比较时候, 扮演先前输入角色

V: 用于计算当前注意力焦点的输出时候, 扮演值角色

自注意力的计算如图:

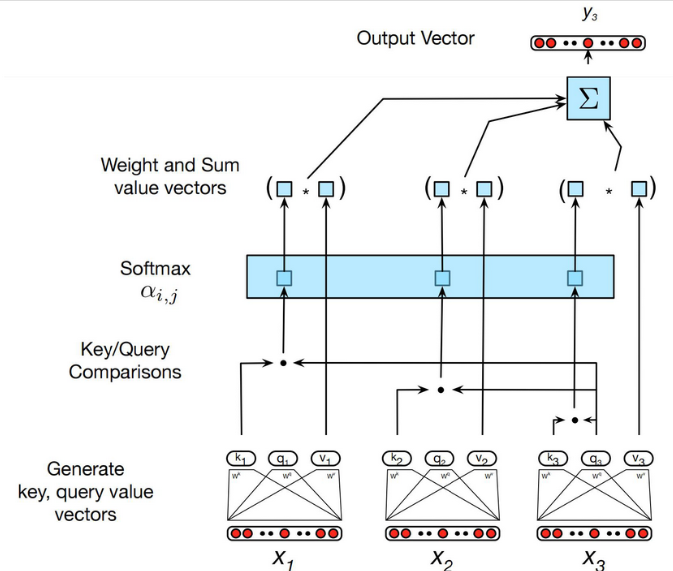
自注意力的计算是Transformer的核心, 处理自注意力机之外, 还包括其它前馈层, 剩余连接和归一化层, 一个典型的Transformer模块如下:

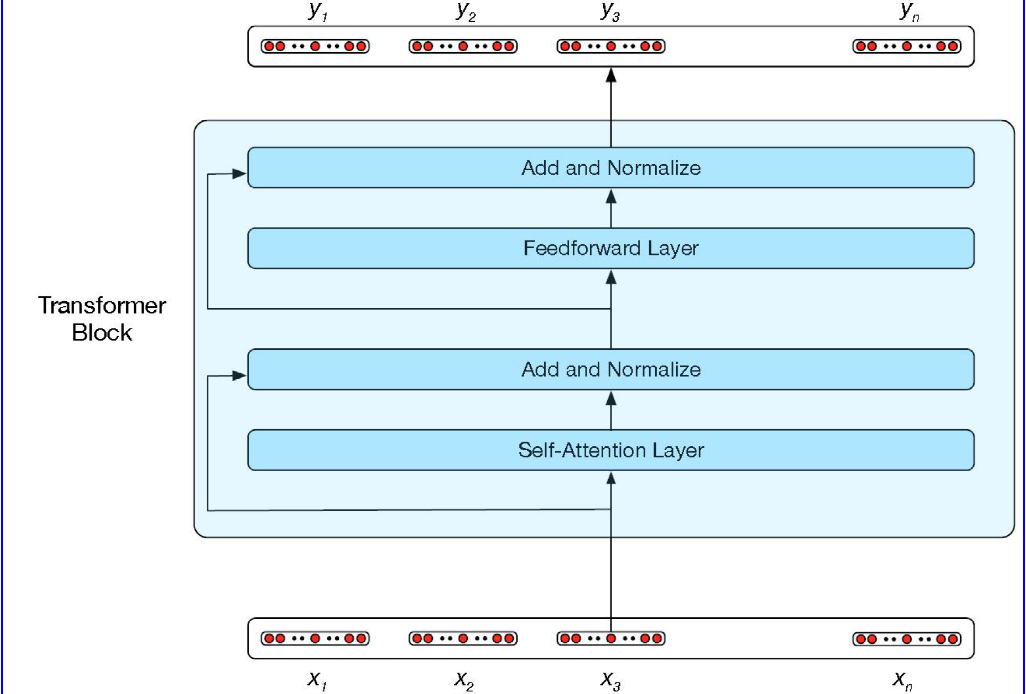
Transformer可以用作自回归语言模型和上下文生成和摘要.

问题
中文和英文是两种类型的语言, 英文更像是一种”解释性”语言, 它存在着大量的从句用来解释说明前面的重点, 比如直译为”我吃了饭位于新餐厅今天”, 但是中文不一样, 中文是一种”形容”式的语言, 比如”今天我吃了新餐厅的饭”, 也就是说, 不同的语言对应的语法任务的sota模型是否应该是不同的, 比如Transformer更适合于英语, 因为左右的上下文信息都很重要, 但是RNN更适合于中文, 因为左的上下文信息对于任务的重要程度逐渐大于右侧的上下文信息?

欢迎在评论区中进行批评指正，转载请注明来源，如涉及侵权，请联系作者删除。