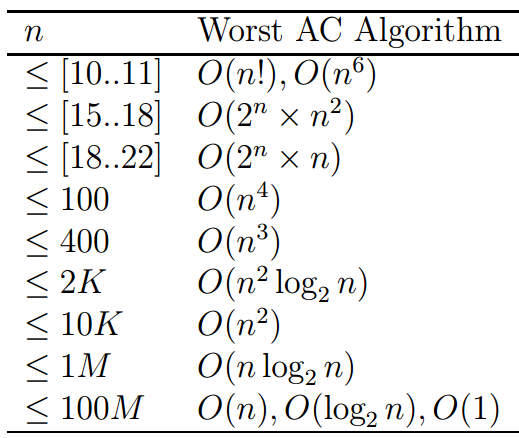
Leetcode时间限制
注意:
⏰表示未完成
⭐表示重要
🌟表示超级重要
😄表示我的思路并且通过了
😭表示自己尝试的方法但是通不过
🙆♂表示他人的方法通过了
🙅♂表示他人的方法但没通过
💭表示只写了想法没写代码无论自己或者其他人的.
题号.题目
描述
样例
思想1名称(self
思路
描述
代码
\\语法, 以后搜索\\语法可以学习语法
\\思想, 学习思想
复杂度
- 时间: $$
- 空间: $$
思想2名称*
思路
描述
代码
复杂度
- 时间: $$
- 空间: $$
LeetCode热题Hot100
2. (M)两数相加 (M)
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
模拟人工加法(self
思路
这道题其实就是链表逆向存储了十进制数, 也就是头存储的是个位, 模拟人工进行加法. 算法实际实现有点归并的思想.但是没有结合成统一的代码, 如果想结合成统一的代码. 就是在节点为空时, 相当于此节点的值为0即可.
代码
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode head = new ListNode();
ListNode cur = head;
int carry = 0;
int num = 0;
while(l1!=null&&l2!=null){
num = (l1.val+l2.val+carry)%10; //思想, 先计算num, 两数之和加进位再对10取余
carry = (l1.val+l2.val+carry)>=10?1:0; //思想, 如果这次相加大于等于10的话下一个进位是1否则为0
ListNode node = new ListNode(num);
cur.next = node;
cur = cur.next; //思想, 下面移动
l1 = l1.next;
l2 = l2.next;
}
while(l1!=null){
num = (l1.val+carry)%10;
carry = (l1.val+carry)>=10?1:0;
ListNode node = new ListNode(num);
cur.next = node;
cur = cur.next;
l1 = l1.next;
}
while(l2!=null){
num = (l2.val+carry)%10;
carry = (l2.val+carry)>=10?1:0;
ListNode node = new ListNode(num);
cur.next = node;
cur = cur.next;
l2 = l2.next;
}
if (carry==1) { //思想, 如果最后一位还有进位的话需要构造
ListNode node = new ListNode(carry);
cur.next = node;
}
return head.next;
}
}
复杂度
- 时间: $O(max{M,N})$
- 空间: $O(max{M,N})$, 其实可以为O(1), 也就是直接在原节点修改.
迭代(self
思路
确定以下:
- 函数干什么: 返回两个数字十进制相加后的新的节点
- 传递参数: 两个数字以及上次的进位, 第一次进位为0
- 终止条件:
- 两个数字都为空
- 其中一个数字为空
- 两个数字都不为空
代码
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
return addTwoNumbersHelp(l1, l2, 0);
}
private ListNode addTwoNumbersHelp(ListNode l1, ListNode l2, int carry){
if (l1==null && l2==null) {
if(carry==1) return new ListNode(1);
return null;
}
else if(l1==null&&l2!=null) {
int num = (l2.val+carry)%10;
carry = l2.val+carry>=10?1:0;
l2.val = num;
l2.next = addTwoNumbersHelp(l1, l2.next, carry);
return l2;
}else if(l1!=null&&l2==null) {
int num = (l1.val+carry)%10;
carry = l1.val+carry>=10?1:0;
l1.val = num;
l1.next = addTwoNumbersHelp(l1.next, l2, carry); //思想
return l1;
}else{
int num = (l1.val+l2.val+carry)%10;
carry = (l1.val+l2.val+carry)>=10?1:0;
l1.val = num;
l1.next = addTwoNumbersHelp(l1.next, l2.next, carry); //思想
return l1;
}
}
}
复杂度
- 时间: $O(max{N,M})$(N和M为两个节点存储十进制数的位数的长度)
- 空间: $O(1)$
3. (M)无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
动态规划(self, 想错方向
思路
本来我的思路是用动态规划的思路, 源自于53题最大子序和, 也就是令
$$
f(i)表示以第i个字母结尾的字符串的长度 \
f(i) = f(i-1)+1 \ \ \ \ \ \ 当i和i-1的字母不相同时 \
max = Math.max(f(1), f(2), …,f(n))
$$
但是我发现这样很难计算当$i$个字母在之前出现过的时候,所以会出现各种问题.
滑动窗口*
思路
两个指针, 一个指针指向窗口的左端, 表示第i个字母时, 不含重复字符子串的左端, 一个指针为i, 表示滑动窗口的右端.
i从0开始, 一次加1,
left默认为0, 当第i个字母没出现时不变, 出现时, 指向这个出现字母最后一次出现的位置+1和left之中最大的那个.
代码
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> m = new HashMap<>();
int max = 0;
int left = 0;
for(int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (m.containsKey(c)) {
left = Math.max(m.get(c)+1, left); //思想
}
m.put(c,i); //思想
max = Math.max(max, i-left+1);
}
return max;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
思想1名称(self
思路
描述
代码
\\语法, 以后搜索\\语法可以学习语法
\\思想, 学习思想
复杂度
- 时间: $$
- 空间: $$
合并排序取中位数*
思路
合并两个数组然后取中位数
但是这个的时间是借sort算法快排的$O(log(M+N))$来实现的, 而不是真正自己实现了所需要的算法复杂度.
代码
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n1 = nums1.length;
int n2 = nums2.length;
int[] nums = new int[n1 + n2];
System.arraycopy(nums1, 0, nums, 0, n1); //语法
System.arraycopy(nums2, 0, nums, n1, n2); //语法
Arrays.sort(nums); //语法
int n = nums.length;
if (n % 2 == 0) {
return (nums[(n/2)-1] + nums[n/2])/2.0;
} else {
return nums[n/2];
}
}
}
复杂度
- 时间: $$
- 空间: $$
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
对折比较相等(self
思路
移动一个指针, 再让这个指针往左走和往右走如果一直想等的话就是回文串, 记录最大长度和这个指针的位置, 要注意, 分为奇对称和偶对称
- 奇对称: abacd, 这个aba以b为对称轴
- 偶对称: abbac, abba以”空”为对称轴
代码
class Solution {
public String longestPalindrome(String s) {
char []str = s.toCharArray();
int max_length = 1; //记录整个回文串的最大长度
int flag = 1; //记录是哪种情况, 1是奇对称(aba), 0是偶对称(aa)
int index = 0; //如果是奇对称, 记录对称轴的位置, 如果是偶对称, 记录空的下一个字符的位置, 这里记录后面那个字符的话就要使得`length>=max_length`
String result = s.substring(0,1);
for(int i =1; i < str.length; i++) {
//奇对称
int length = 1; //奇对称初始长度为1
for(int j = i-1, k = i+1; j >=0&&k<str.length;j--,k++){
if(str[j]==str[k]) {
length+=2;
if(length>=max_length) {
index = i;
flag = 1;
max_length = length;
}
}else{
break;
}
}
//偶对称
length = 0; //偶对成初始长度为0
for(int j = i-1,k = i; j >=0 && k < str.length; j--, k++) {
if(str[j]==str[k]) {
length+=2;
if(length>=max_length) {
index = i;
flag = 0;
max_length = length;
}
}else{
break;
}
}
}
if (flag == 0) {
//abbacd的话, index就是第二个b, max_length是4
result = s.substring(index-max_length/2,index+max_length/2);
}else{
//abcbad, index是c, max_length是5.
result = s.substring(index-max_length/2, index+max_length/2+1);
}
return result;
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(N)$, 浪费这么多空间主要是为了直接用[]取字符, 使用s.charAt也可以做到$O(1)$.
10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
递归(self, 只过了一半样例, 没做出来
思路
慢慢的确定终止条件再到一半情况
代码
class Solution {
public boolean isMatch(String s, String p) {
if (s.length()==0&&p.length()==0) {
return true;
}else if(s.length()==0&&p.length()==1){ //s是空串, p不为空的情况
return false;
}else if(s.length()==0&&p.length()>1){
char c1 = p.charAt(0);
char c2 = p.charAt(1);
if (c2=='*') { //如果是"p*"或者".*"这种情况
return isMatch(s, p.substring(2,p.length()));
}else{ //如果是"a"这种情况
return false;
}
}else if(s.length() > 0 && p.length() ==0) { //s不是空串,但是p是空串
return false;
}else if(s.length() >0 && p.length() ==1) {
char c = s.charAt(0);
char c1 = p.charAt(0);
if ((c==c1||c1=='.')&&s.length()==1) return true;
else return false;
}else{
char c = s.charAt(0);
char c1 = p.charAt(0);
char c2 = p.charAt(1);
if(c==c1||c1=='.') {
if(c2=='*'){
return isMatch(s.substring(1,s.length()), p);
}else{
return isMatch(s.substring(1,s.length()), p.substring(1,p.length()));
}
}else{
if(c2=='*'){
return isMatch(s, p.substring(2,p.length()));
}else{
return false;
}
}
}
}
}
错误原因:
通过测试用例:298 / 353
输入:
"aaa"
"a*a"
输出:
false
预期结果:
true
我只是从前匹配, 但是a*到底要匹配多少次这是从前匹配做不到的.
动态规划*
思路
还没学习呢
代码
复杂度
- 时间: $$
- 空间: $$
11. 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器。
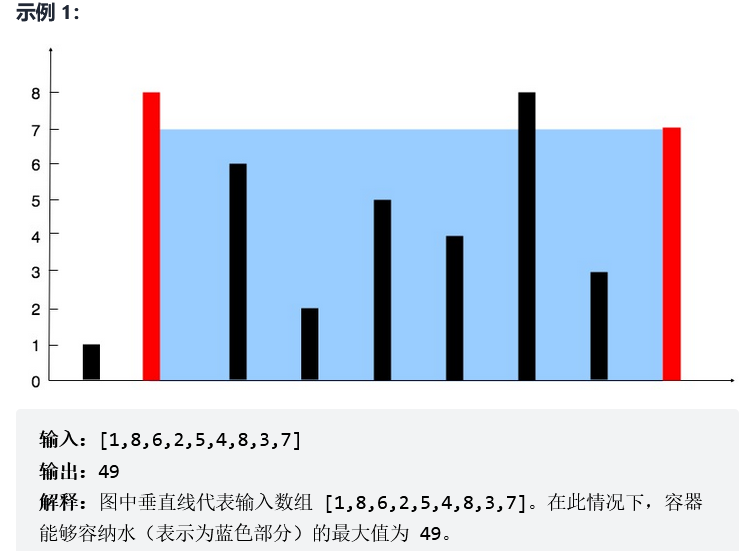
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
双指针
思路
这题一看数据量, $10^5$表明$n^2$的暴力群举就会超时, 所以要想其他办法, 先写出动态规划方程:
$$
max_area = max( min(height[i],height[j])*(j-i))
$$
问题就出现在宽和高上, 宽虽然一次移动1个单位, 但是面积的增加与否还要看移动后的高是否会减小, 我的想法就这么中断了, 因为我不知道如何判断移动后的高是不是正确的高, 但其实不用管是不是正确的高, 我们只需要记录最大的面积就好了, 尽管它不是正确的高, 只要我们遍历所有情况, 记录最大的面积就可以了.
接下来就写循环, 如果都从一端开始, 一个是循环终止不好写, 另一个是i和j都从一端开始的话必然$N^2$, 所以技巧就在于用双指针刚开始指向首尾, 然后移动这两个指针中的一个, 移动哪一个呢?移动那个高比较短的那个的下标.
代码
class Solution {
public int maxArea(int[] height) {
int area = 0;
int i = 0;
int j = height.length-1; //思想, 双指针指向首尾
area = Math.min(height[i],height[j])*(j-i);
while(i!=j) {
if(height[i]<=height[j]) i++;
else j--;
int new_area = Math.min(height[i],height[j])*(j-i);//思想,动态规划方程
if (new_area>area) {
area = new_area;
}
}
return area;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
15. 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
示例 2:
输入:nums = [-1,3,2,-1,0,0]
输出:[[-1,-1,2],[2,3,-1],[3,0,0]]
注意: 这里的数字可以用多次, 只是最后的结果不能重复而已.
示例 3:
输入:nums = [-1,0,-1,0]
输出:[[-1,0,1]]
注意: 没有[0,0,0]这个答案
提示:
0 <= nums.length <= 3000-105 <= nums[i] <= 105
双循环+map计数+set存储(self
思路
一看数据量, 说明$n^2$算法可以解决, 所以是两个循环, 第三个数用map来直接查找.
首先要明确的是这里面的数字可以用多次, 只是结果里面的不能重复而已, 所以结果需要用一个set<>先存储, 另外, 里面的小结果不能用set<Integer>存储, 因为可能出现[1, 1, -2]这种答案, 所以, 最后答案的存储要用set<List<Integer>>来存储, 并且在将list<Integer>放入set前要进行排序, 否则发挥不了set的作用.
代码
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for(int i = 0; i <nums.length; i++) {
map.put(nums[i],map.getOrDefault(nums[i],0)+1);
}
Set<List<Integer>> answer = new HashSet<>();
List<List<Integer>> result = new ArrayList<>();
if(nums.length < 3) return result; //思想, 小于3的答案为空直接返回.
for(int i = 0; i < nums.length; i++) {
for (int j = i+1; j < nums.length; j++) {
int last_num = 0-nums[i]-nums[j];
if(nums[i]==last_num&&map.get(nums[i])>=2&&last_num!=nums[j]&&map.get(nums[j])>=1) {
//[-1,-1,2,0]这种情况,两个相同
}
else if(nums[j]==last_num&&map.get(nums[j])>=2&&last_num!=nums[i]&&map.get(nums[i])>=1) {
//[-1,-1,2,0]这种情况
}else if(nums[i]!=last_num&&nums[j]!=last_num&&map.get(nums[i])>=1&&map.get(nums[j])>=1&&map.getOrDefault(last_num,0)>=1) {
//[1,2,-3]这种情况,都不相同(一个相同)
}else if(nums[i]==last_num&&nums[j]==last_num&&map.get(nums[i])>=3){
//[0,0,0]这种情况, 三个相同
}
else{
continue;
}
List<Integer> new_answer = new ArrayList<>();
new_answer.add(nums[i]);
new_answer.add(nums[j]);
new_answer.add(last_num);
Collections.sort(new_answer); //思想, //语法,在进set前进行排序
answer.add(new_answer);
}
}
for(List<Integer> new_set:answer) {
List<Integer> new_result = new ArrayList<>(new_set);
result.add(new_result);
}
return result;
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(N)$
排序+双指针*
思路
本题的难点在于如何去除重复解。
- 特判,对于数组长度 nnn,如果数组为 nulll或者数组长度小于 3,返回 [][][]。
- 对数组进行排序。
- 遍历排序后数组:
- 若 nums[i]>0:因为已经排序好,所以后面不可能有三个数加和等于 0,直接返回结果。
- 如果nums[i]与nums[i-1]相同, 继续(排除重复解)
- 令左指针 L=i+1,右指针 R=n−1,当 L<R时,执行循环:
- nums[i]+nums[L]+nums[R]==0时, 执行循环, 如果左指针和下一个位置相同, 则前进(排除相同解)或者右指针的前一个位置相同,则前进
- 若和大于0, 说明nums[R]太大, R左移
- 若和小于0, 说明nums[L]太小, L右移
最后两句话是精髓!
代码
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> lists = new ArrayList<>();
//排序
Arrays.sort(nums);
//双指针
int len = nums.length;
for(int i = 0;i < len;++i) {
if(nums[i] > 0) return lists;
if(i > 0 && nums[i] == nums[i-1]) continue;
int curr = nums[i];
int L = i+1, R = len-1;
while (L < R) {
int tmp = curr + nums[L] + nums[R];
if(tmp == 0) {
List<Integer> list = new ArrayList<>();
list.add(curr);
list.add(nums[L]);
list.add(nums[R]);
lists.add(list);
while(L < R && nums[L+1] == nums[L]) ++L;
while (L < R && nums[R-1] == nums[R]) --R;
++L;
--R;
} else if(tmp < 0) {
++L;
} else {
--R;
}
}
}
return lists;
}
复杂度
- 时间: $O(N^2$)
- 空间: $O(1)$
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
示例 1:
输入:digits = "23"
输出:["ad","ae","af","bd","be","bf","cd","ce","cf"]
递归+循环(self
思路
递归的终止条件是当传递的字符串为0.
递归的传递参数是字符串.
递归的返回类型是List
因为数字和字母的对应关系不是规则的, 所以为了解决这个问题写了很多没有算法思想的语句.
但从这个思想上, 我们已经看到了本题应该使用回溯算法思想.
代码
class Solution {
public List<String> letterCombinations(String digits) {
if(digits.length()==0) return new ArrayList<String>();
return letterCombinationsHelp(digits);
}
private List<String> letterCombinationsHelp(String digits) {
List<String> result = new ArrayList<>();
if(digits.length()==0) {
result.add("");
return result;
}
List<String> lastList = new ArrayList<>();
lastList = letterCombinationsHelp(digits.substring(1,digits.length()));
if(digits.charAt(0)>='2'&&digits.charAt(0)<='6') {//0-6可以
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'2')*3+'a'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'2')*3+'b'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'2')*3+'c'))+item);
}
}else if(digits.charAt(0)=='7'){
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'7')+'p'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'7')+'q'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'7')+'r'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'7')+'s'))+item);
}
}else if(digits.charAt(0)=='8'){
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'8')+'t'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'8')+'u'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'8')+'v'))+item);
}
}else if(digits.charAt(0)=='9') {
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'9')+'w'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'9')+'x'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'9')+'y'))+item);
}
for(String item:lastList) {
result.add((char)(((digits.charAt(0)-'9')+'z'))+item);
}
}
return result;
}
}
复杂度
- 时间: $O(N)$, N层递归, 每层递归最多10次操作左右, 好像不是很准确
- 空间: $O(N)$, N层递归
回溯*
思路
描述
代码
class Solution {
public List<String> letterCombinations(String digits) {
List<String> combinations = new ArrayList<>();
if(digits.length()==0) return combinations;
Map<Character, String> phoneMap = new HashMap<>(){{
put('2', "abc");
put('3', "def");
put('4', "ghi");
put('5', "jkl");
put('6', "mno");
put('7', "pqrs");
put('8', "tuv");
put('9', "wxyz");
}};
backtrack(combinations, phoneMap, digits, 0, new StringBuffer());
return combinations;
}
private void backtrack(List<String> combinations, Map<Character, String> phoneMap, String digits, int index, StringBuffer combination) {
if (index == digits.length()) {
combinations.add(combination.toString());
}else {
char digit = digits.charAt(index);
String letters = phoneMap.get(digit);
for(int i = 0; i < letters.length(); i++) {
combination.append(letters.charAt(i));
backtrack(combinations, phoneMap, digits, index+1, combination);
combination.deleteCharAt(index);
}
}
}
}
复杂度

19. 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
快慢指针(self
思路
双指针, 先移动第二个指针到倒数第n个位置,然后两个指针一起移动, 第二个指针移动到末尾的时候第一个指针指向倒数第n个位置.
具体还用了一个技巧, 就是p指向倒数第n+1个位置, 这样好删除.
代码
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode fakeHead = new ListNode();
fakeHead.next = head;
ListNode result = fakeHead;
ListNode p = fakeHead;
ListNode q = fakeHead;
int i = 0;
while(i<=n) {
i++;
q = q.next;
}
while(q!=null) {
p = p.next;
q = q.next;
}
p.next = p.next.next;
return result.next;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 2
输出:["()()", "(())" ]
示例 3:
输入:n = 1
输出:["()"]
递归+迭代加括号(self
思路
从n=1到n=3我得出规律, 每个n都是n-1的字符串的前, 外, 后上面加括号, 比如
n = 1 ()
n = 2 ()() (()) ()()[这个去重]
但是写好代码发现, n=4由n=3前外后加括号会遗漏一个答案, 就是这个(())(()), 显然这个答案无法从n=3的答案中前外后加括号所得到, 也就是我的刚开始想的递归方程是错误的, 代码如下:
private Set<String> generateParenthesisHelp(int n) {
Set<String> set = new HashSet<>();
if(n == 0) {
set.add("");
return set;
}else {
Set<String> lastSet = generateParenthesisHelp(n-1);
for(String item:lastSet) {
String new_item1 = "()"+item;
String new_item2 = "("+item+")";
String new_item3 = item+"()";
set.add(new_item1);
set.add(new_item2);
set.add(new_item3);
}
return set;
}
}
其实递归方程应该是对于n-1的串, 遍历他们, 然后增加item.substring(0,i)+"()"+item.substring(i,item.length())这样.
代码
class Solution {
public List<String> generateParenthesis(int n) {
List<String> result = new ArrayList<>(generateParenthesisHelp(n));
return result;
}
private Set<String> generateParenthesisHelp(int n) {
Set<String> set = new HashSet<>();
if(n == 1) {
set.add("()");
return set;
}else {
Set<String> lastSet = generateParenthesisHelp(n-1);
for(String item:lastSet) {
for(int i = 0; i < item.length(); i++) {
set.add(item.substring(0,i)+"()"+item.substring(i,item.length()));
}
}
return set;
}
}
}
复杂度
- 时间: $O(N*2^{N-1})$
- 空间: $O(2^{N-1})$
思想2名称*
思路
描述
代码
复杂度
- 时间: $$
- 空间: $$
23. 合并K个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
存放数组排序后形成链表(self
思路
存放数组排序后形成链表返答案
代码
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
List<Integer> result = new ArrayList<>();
for(int i = 0; i < lists.length; i++) {
ListNode p = lists[i];
while(p!=null) {
result.add(p.val);
p = p.next;
}
}
Collections.sort(result);
ListNode fakeHead = new ListNode();
ListNode p = fakeHead;
for(int i = 0; i < result.size(); i++) {
ListNode node = new ListNode(result.get(i));
p.next = node;
p = p.next;
}
return fakeHead.next;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$(算返回的时间)
分治*(self
思路
这其实就是多路归并, 但是因为多路归并的比较不如二路归并那么快, 所以要把多路归并转化为二路归并, 也就是分治算法, 但是我的这个分治写的不是标准的分治, 标准的分治不会复制形成新的节点, 而是在原有的节点的基础上, 用左右两个指针指代需要分治的位置.
代码1
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return divideAndConquer(lists);
}
ListNode divideAndConquer(ListNode[] lists) {
//分治
if(lists.length == 0) return null;
if(lists.length == 1) {
return lists[0];
}
ListNode fakeHead = new ListNode();
ListNode p = fakeHead;
ListNode[] lists1 = new ListNode[lists.length/2];
ListNode[] lists2 = new ListNode[lists.length-lists.length/2];
System.arraycopy(lists, 0, lists1, 0, lists.length/2);
System.arraycopy(lists, lists.length/2, lists2, 0, lists.length-lists.length/2);
ListNode node1= divideAndConquer(lists1);
ListNode node2 = divideAndConquer(lists2);
//合并
while(node1!=null&&node2!=null) {
if(node1.val<=node2.val) {
p.next = node1;
node1 = node1.next;
}else{
p.next = node2;
node2 = node2.next;
}
p = p.next;
}
if(node1!=null) p.next = node1;
if(node2!=null) p.next = node2;
return fakeHead.next;
}
}
代码2
对代码1的分治进行了改进, 节省了空间, 比较标准化写了分治
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
return divideAndConquer(lists,0,lists.length);
}
ListNode divideAndConquer(ListNode[] lists, int left, int right) {
if(left==right) return null;
if(right-left == 1) {
return lists[left];
}
ListNode fakeHead = new ListNode();
ListNode p = fakeHead;
ListNode node1= divideAndConquer(lists, left, left+(right-left)/2);
ListNode node2 = divideAndConquer(lists, left+(right-left)/2, right);
while(node1!=null&&node2!=null) {
if(node1.val<=node2.val) {
p.next = node1;
node1 = node1.next;
}else{
p.next = node2;
node2 = node2.next;
}
p = p.next;
}
if(node1!=null) p.next = node1;
if(node2!=null) p.next = node2;
return fakeHead.next;
}
}
复杂度

优先队列(self
思路
官方题解用优先队列来取代二路归并的比较进行多路归并的比较, 但是我想着都用优先队列了, 直接遍历数据存入优先队列(自然排序)再形成链表自然就是答案了.
代码
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<Integer> queue = new PriorityQueue<Integer>();
for(int i = 0; i < lists.length; i++) {
ListNode node = lists[i];
while(node!=null) {
queue.add(node.val);
node = node.next;
}
}
ListNode fakeHead = new ListNode();
ListNode p = fakeHead;
int len = queue.size(); //语法, 优先队列的按自然排序取出只能这样取,因为是堆排序, 每出来一个大小会变化.
for(int i = 0; i < len; i++) {
p.next = new ListNode(queue.poll());
p = p.next;
}
return fakeHead.next;
}
}
复杂度
- 时间: $O(NNlog^N)$遍历N遍, 每遍进行一次堆排序
31. 下一个排列
整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。
例如,arr = [1,2,3] ,以下这些都可以视作 arr 的排列:[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。
整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。如果不存在下一个更大的排列,那么这个数组必须重排为字典序最小的排列(即,其元素按升序排列)。
示例 1:
输入:nums = [1,2,3]
输出:[1,3,2]
示例 2:
输入:nums = [3,2,1]
输出:[1,2,3]
下一个排列算法
思路
从后往前一直顺序, 顺序被打断的位置记作$little_small_index$, 然后在$(little_small_index, length-1)$中找比little_small_index位置的最小的稍大数(因为little_small_index,length-1)是顺序, 所以从后往前或者从前往后遍历一遍就找到了, 位置记作little_big_index), 交换little_small_index和little_big_index, 然后再对little_small_index后的进行一遍排序(也就是转置, 因为交换后的(little_small_index, length-1)依然是顺序.
代码
class Solution {
public void nextPermutation(int[] nums) {
if(nums.length==1) return;
int flag = 0; //标志,0表示从后往前顺序,-1表示被打断
int little_small_index = 0;
int little_big_index = 0;
for(int i = nums.length-1; i > 0; --i) { //思想, 找到稍微小一点的index
if(nums[i]<=nums[i-1]) {
//从后往前顺序
continue;
}else{
flag = 1;
little_small_index = i-1;
break;
}
}
for (int i = nums.length-1; i > little_small_index; --i) {//思想,找到稍微大一点的index
if(nums[i] <= nums[little_small_index]) continue;
else {
little_big_index = i;
break;
}
}
if(flag == 0) {
//从后往前一直顺序
inverse(nums, 0, nums.length-1);
}else {
swap(nums, little_small_index, little_big_index);
inverse(nums, little_small_index+1, nums.length-1);
}
return;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
return;
}
private void inverse(int[] nums, int s, int e) { //语法, 原地转置
for(int i = 0; i <= (e-s)/2;i++) {
swap(nums, s+i,e-i);
}
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
示例 4:
输入:s = "()(()"
输出:2
示例 3:
输入:s = ")()())"
输出:4
动态规划
思路
见题解
代码
class Solution {
public int longestValidParentheses(String s) {
int [] dp = new int[s.length()];
int max_length = 0;
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i)==')'){
if(s.charAt(i-1)=='(') {
dp[i] = (i>=2?dp[i-2]:0)+2; //语法, //思想, 这里的三目运算符是为了解决dp初始化问题和边界问题.
}else if(i-dp[i-1]>0 && s.charAt(i-dp[i-1]-1)=='(') {
dp[i] = dp[i-1]+ (i-dp[i-1]>=2 ? dp[i-dp[i-1]-2]:0)+2; //语法, //思想, 这里的三目运算符是为了解决dp初始化问题和边界问题.
}
max_length = max_length < dp[i]?dp[i]:max_length;
}
}
return max_length;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
33. 搜索旋转排序数组
整数数组 nums 按升序排列,数组中的值 互不相同 。
在传递给函数之前,nums 在预先未知的某个下标 k(0 <= k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]](下标 从 0 开始 计数)。例如, [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。
给你 旋转后 的数组 nums 和一个整数 target ,如果 nums 中存在这个目标值 target ,则返回它的下标,否则返回 -1 。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
提示:
- 1 <= nums.length <= 5000
- -10^4 <= nums[i] <= 10^4
- nums 中的每个值都 独一无二
- 题目数据保证 nums 在预先未知的某个下标上进行了旋转
- -10^4 <= target <= 10^4
顺序遍历(self
思路
这个题数据量O(N)能解决, 所以先直接顺序遍历找AC后再思考考点.
考点应该是如果数据量超大的话必须降为$O(logN)$, 如果是对数时间复杂度, 寻找的复杂度用二分即可实现, 但是要找到那个旋转点 k 才能进行二分, 所以找k的算法应该也是对数复杂度.可以这样找k
- 将nums对半分, 这样一个必定为顺序, 一个必定为旋转数组
- 回到上步
代码
class Solution {
public int search(int[] nums, int target) {
int result = -1;
for(int i = 0; i < nums.length; i++) {
if(target == nums[i]) {
result = i;
break;
}
}
return result;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
二分查找变体(self
思路
二分寻找的变体.
- 先分为两半, 必定一个顺序一个旋转
- 如果target在顺序之中, 则继续寻找, 否则在旋转中寻找
- 寻找的终止条件是e-s<=1 , 也就是一个数或者两个数(一般来说为一个数, 但是有点数组越界, 我就改造了一下)
代码
class Solution {
public int search(int[] nums, int target) {
return binarySearch(nums, 0, nums.length-1, target);
}
private int binarySearch(int[] nums, int s, int e, int target) {
int m = s + (e-s)/2;
if (e-s<=1) {
if (nums[s]==target) return s;
else if(nums[e]==target) return e;
else return -1;
}
if (nums[s] < nums[m]) {
if (nums[s]<=target &&nums[m]>=target) return binarySearch(nums, s, m, target);
else{
return binarySearch(nums, m, e, target);
}
}else{
if (nums[m]<=target &&nums[e]>=target) return binarySearch(nums, m, e, target);
else{
return binarySearch(nums, s, m, target);
}
}
}
}
复杂度
- 时间: $O(logN)$
- 空间: $O(1)$
34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
二分查找变体(self
思路
两个二分查找, 只不过一个从前找start, 一个从后找end.
代码
class Solution {
public int[] searchRange(int[] nums, int target) {
int [] result = new int[2];
result[0] = -1;
result[1] = -1;
if (nums.length==0) return result;
result[0] = binarySearchStart(nums, 0, nums.length-1, target);
result[1] = binarySearchEnd(nums, 0, nums.length-1, target);
return result;
}
// 找start
public int binarySearchStart(int[] nums, int s, int e, int target) {
if(e-s<=1) {
if(nums[s] == target) return s;
else if(nums[e] == target) return e;
else return -1;
}
int m = s+(e-s)/2;
if(nums[s]<=target && target <= nums[m]) return binarySearchStart(nums, s, m, target);
else return binarySearchStart(nums, m+1, e, target);
}
public int binarySearchEnd(int[] nums, int s, int e, int target) {
if(e-s<=1) {
if(nums[e] == target) return e;
else if(nums[s] == target) return s;
else return -1;
}
int m = s+(e-s)/2;
if(nums[m]<=target && target <= nums[e]) return binarySearchEnd(nums, m, e, target);
else return binarySearchEnd(nums, s, m-1, target);
}
}
代码2
class Solution {
public int[] searchRange(int[] nums, int target) {
int [] result = new int[2];
result[0] = -1;
result[1] = -1;
if (nums.length==0) return result;
result[0] = binarySearchStart(nums, 0, nums.length-1, target);
result[1] = binarySearchEnd(nums, 0, nums.length-1, target);
return result;
}
public int binarySearchStart(int[] nums, int s, int e, int target) {
if(e-s==0) {
if(nums[s] == target) return s;
else return -1;
}
int m = s+(e-s)/2;
if(nums[s]<=target && target <= nums[m]) return binarySearchStart(nums, s, m, target);
else return binarySearchStart(nums, m+1, e, target);
}
public int binarySearchEnd(int[] nums, int s, int e, int target) {
if(e-s==0) {
if(nums[e] == target) return e;
else return -1;
}
int m = s+(e-s)/2+1; //注意这里要+1.
if(nums[m]<=target && target <= nums[e]) return binarySearchEnd(nums, m, e, target);
else return binarySearchEnd(nums, s, m-1, target);
}
}
复杂度
- 时间: $O(logN)$
- 空间: $O(1)$
39. 组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
回溯(self, 没做出来
思路
就一看就是回溯的题, 但对回溯的方法不太熟, 只能写个大概.
代码
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> last = new ArrayList<>();
combinationSumHelp(candidates, target, 0, last, 0, result);
return result;
}
public void combinationSumHelp(int[] candidates, int target, int index, List<Integer> last, int sum, List<List<Integer>> result) {
if(index >= candidates.length) return;
if(candidates[index]+sum==target) {
last.add(candidates[index]);
sum+=candidates[index];
List<Integer> result_item = new ArrayList<>(last);
result.add(result_item);
return;
}else if(candidates[index]+sum > target) {
return;
}
else if(candidates[index]+sum < target){
last.add(candidates[index]);
List<Integer> temp_last = new ArrayList<>(last);
combinationSumHelp(candidates, target, index, temp_last, sum+=candidates[index], result);
last.remove(last.size()-1);
sum-=candidates[index];
combinationSumHelp(candidates, target, index+1, last, sum, result);
}
}
}
回溯*
思路
描述
代码
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> combination = new ArrayList<>();
combinationSumHelp(candidates, target, 0, combination, result);
return result;
}
public void combinationSumHelp(int[] candidates, int target, int begin, List<Integer> combination, List<List<Integer>> result) {
if (target < 0) return;
if (target == 0) {
result.add(new ArrayList<>(combination));
return;
}
for (int i = begin; i < candidates.length; i++) {
combination.add(candidates[i]);
combinationSumHelp(candidates, target-candidates[i], i, combination, result);
combination.remove(combination.size()-1);
}
}
}
复杂度
- 时间: $O(S)$,其中 S为所有可行解的长度之和(树的深度之和, 可以通过剪枝来降低)
- 空间: $O(target)$, 最差为target深(都是1).
46. 全排列
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
填空(self没做出来
思路
我想的是[1, 2, 3, 4], 然后把1取出来, 然后放入剩下的[2, 3, 4]的四个空中, 这样遍历所有数据来一次.
这么做不能得到全排列, 比如[4, 3, 2, 1]这个数据出不来, 只能出来[4, 1, 2, 3], [1, 4, 2, 3], [1, 2, 4, 3], [1, 2, 3, 4]这些数据
回溯*
思路
描述
代码
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> collections = new ArrayList<>();
List<Integer> collection = new ArrayList<>();
int [] flags = new int[nums.length]; //用一个flag数组来标志是否使用过
int depth = nums.length;
dfs(collections, collection, nums, flags, depth, 0);
return collections;
}
//思想
void dfs(List<List<Integer>> collections, List<Integer> collection, int[]nums, int [] flags, int depth, int index){
if (index == depth) {
collections.add(new ArrayList<Integer>(collection));
return;
}
for (int i = 0; i < depth; i++) {
if (flags[i] == 0) {
flags[i] = 1;
collection.add(nums[i]);
dfs(collections, collection, nums, flags, depth, index+1);
flags[i] = 0;
collection.remove(collection.size()-1);
}
}
}
}
复杂度
- 时间: $O(N*N!)$
- 空间: $O(N)$
48. 旋转图像
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
利用矩阵的转置加镜像*
思路
转置和镜像可以原地进行.
向右旋转90°=>先转置再左右镜像.
向右旋转180°=>先左右镜像, 再上下镜像.
向右旋转270°=>先转置再上下镜像(也就是向左旋转90°)
代码
class Solution {
public void rotate(int[][] matrix) {
transpose(matrix);
leftRightMirror(matrix);
return;
}
void transpose(int[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
for (int j = i; j < matrix.length;j++) {
int t = matrix[i][j];
matrix[i][j] = matrix[j][i];
matrix[j][i] = t;
}
}
return;
}
void leftRightMirror(int [][]matrix) {
for (int j= 0; j< matrix.length/2; j++) {
for (int i = 0; i < matrix.length; i++) {
int t = matrix[i][j];
matrix[i][j] = matrix[i][matrix.length-1-j];
matrix[i][matrix.length-1-j] = t;
}
}
}
void upDownMirror(int [][] matrix) {
for (int i = 0; i < matrix.length/2; i++) {
for (int j = 0 ;j < matrix.length; j++) {
int t = matrix[i][j];
matrix[i][j] = matrix[matrix.length-1-i][j];
matrix[matrix.length-1-i][j] = t;
}
}
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(1)$
49. 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
字母异位词 是由重新排列源单词的字母得到的一个新单词,所有源单词中的字母通常恰好只用一次。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
示例 2:
输入: strs = [""]
输出: [[""]]
Map(self
思路
先得到每个字符串对应的字典序字符串, 然后创建该字典序字符串的map<string, List<String>>, 遍历一遍放进去之后再遍历一遍得到列表.
代码
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
List<String> lexicographicOrderStrs = new ArrayList<>();//对应strs的字典序列表
List<List<String>> result;
for(int i = 0; i < strs.length; i++) {
lexicographicOrderStrs.add(i, getLexicographicOrder(strs[i]));
}
//System.out.println(lexicographicOrderStrs);
Map<String, List<String>> stringMap = new HashMap<>();
for (int i = 0; i < strs.length; i++) {
List<String> item = stringMap.getOrDefault(lexicographicOrderStrs.get(i), new ArrayList<String>());
item.add(strs[i]);
stringMap.put(lexicographicOrderStrs.get(i), item);
}
result = new ArrayList<>(stringMap.values());
return result;
}
String getLexicographicOrder(String str) {
char[] ar = str.toCharArray();
Arrays.sort(ar);
String sortedStr = String.valueOf(ar);
return sortedStr;
}
}
复杂度
- 时间: $O(NKlog^K)$ K为字符串最长长度
- 空间: $O(N)$
代码
官方题解简化版
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String str : strs) {
char[] array = str.toCharArray();
Arrays.sort(array);
String key = new String(array);
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/group-anagrams/solution/zi-mu-yi-wei-ci-fen-zu-by-leetcode-solut-gyoc/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
动态规划?(self
思路
用一个max来记录该位置之前可以到达最远的位置, 然后比较该位置和最远位置, 如果该位置可以到达, 重新计算最远位置, 直至最后一个位置.
代码
class Solution {
public boolean canJump(int[] nums) {
int max = 0+nums[0]; //之前的步数可以到达的最大坐标.
boolean flag = true; //是否可以到达最后下标.
for (int i = 1; i < nums.length; i++) {
if(i <= max) {
//可以到达
max = max > i+nums[i]?max:i+nums[i];
}else {
flag = false; //不可以到达
break;
}
}
return flag;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
56. 合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
输入:intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
解释:区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入:intervals = [[1,4],[4,5]]
输出:[[1,5]]
解释:区间 [1,4] 和 [4,5] 可被视为重叠区间。
示例 3:
输入:intervals = [[1,4],[5,6]]
输出:[[1,4],[5,6]]
解释:区间 [1,4] 和 [5,6] 不可被视为重叠区间。
模拟(self, 没做出来
思路
把各个区间遍历一遍在数轴上进行标记, 然后再遍历一遍数轴得到这些区间.
这个思想是错误的, 这个只能得到合并后的区间, 但是不能得到重叠的区间, 比如示例3, 示例3就会被这样的算法得到一个区间, 没有体现重叠.
代码
class Solution {
public int[][] merge(int[][] intervals) {
int [] flags = new int[10001];
for (int i = 0; i < intervals.length; i++) {
for(int j = intervals[i][0]; j <=intervals[i][1]; j++) {
flags[j] = 1;
}
}
List<List<Integer>> result = new ArrayList<>();
int flag = 0; //是否已经选取左端点的标志
for(int i = 0; i < 10001; i++) {
if(flags[i] == 1 && flag == 0) {
List<Integer> item = new ArrayList<>();
item.add(i);
result.add(item);
flag = 1;
}else if(flags[i] == 1 && flag == 1) {
if (i==10000||flags[i+1]==0) {
//右端
result.get(result.size()-1).add(i);
flag = 0;
}else{
//非右端, 中间
continue;
}
}else {
//flags[i] == 0
continue;
}
}
int[][] realResult = new int[result.size()][2];
for(int i = 0; i < result.size(); i++) {
realResult[i][0] = result.get(i).get(0);
realResult[i][1] = result.get(i).get(1);
}
return realResult;
}
}
排序后找规律*
思路
对这些区间进行左端的排序保证左端一定最小, 然后的话合并这些区间:
- 如果下一个区间的左端比上一个区间的右端大, 一定不重叠, 直接形成新区间.
- 如果下一个区间的左端比上一个区间的右端小, 然后将上一个区间的右端置为这两个区间最大的右端.
代码
class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, new Comparator<int[]>(){//语法
public int compare(int [] intervals1, int [] intervals2) {
return intervals1[0] - intervals2[0];
}
});
List<int[]> merge = new ArrayList<>();
for (int i = 0; i < intervals.length; i++) {
int L = intervals[i][0];
int R = intervals[i][1];
if (merge.size()==0||merge.get(merge.size()-1)[1] < L) {//语法, //思想
merge.add(new int[]{L,R});
}else{
//如果存在重叠
merge.get(merge.size()-1)[1] = Math.max(merge.get(merge.size()-1)[1], R);//思想
}
}
return merge.toArray(new int[merge.size()][]);//语法
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
动态规划(self
思路
把最后一行和最后一列初始化为1, 然后从右下角往左上角计算,动态规划方程如下:
$$
squar[i][j] = 1; (i=m-2, j=1,2…n-1)\
squar[i][j] = 1; (j=n-2, j=1,2…m-1)\
squar[i][j] = square[i][j+1]+square[i+1][j];
$$
代码
class Solution {
public int uniquePaths(int m, int n) {
int [][] square = new int[m][n];
square[m-1][n-1] = 1;
for(int i = 0; i < m; i++) {
square[i][n-1] = 1;
}
for(int j = 0; j < n; j++) {
square[m-1][j] = 1;
}
for (int i = m-2; i >= 0; i--) {
for (int j = n-2; j >= 0; j--) {
square[i][j] = square[i][j+1]+square[i+1][j];
}
}
return square[0][0];
}
}
复杂度
- 时间: $O(M*N)$
- 空间: $O(M*N)$
动态规划*
思路
从左上往右下计算
代码
class Solution {
public int uniquePaths(int m, int n) {
int [][] square = new int[m][n];
square[m-1][n-1] = 1;
for(int i = 0; i < m; i++) {
square[i][n-1] = 1;
}
for(int j = 0; j < n; j++) {
square[m-1][j] = 1;
}
for (int i = m-2; i >= 0; i--) {
for (int j = n-2; j >= 0; j--) {
square[i][j] = square[i][j+1]+square[i+1][j];
}
}
return square[0][0];
}
}
复杂度
- 时间: $O(M*N)$
- 空间: $O(M*N)$
组合数学
思路
一共需要走$m+n-2$步, 需要从中挑选$m-1$次向下移动.
代码
class Solution {
public int uniquePaths(int m, int n) {
long ans = 1;
for (int x = n, y = 1; y < m; ++x, ++y) {
ans = ans * x / y;
}
return (int) ans;
}
}
复杂度
时间复杂度:O(m)。由于我们交换行列的值并不会对答案产生影响,因此我们总可以通过交换 m和 n 使得 m<=n,这样空间复杂度降低至 O(min(m,n))。
空间复杂度:O(1)。
64. 最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
动态规划(self
思路
动态规划, 和63题思路差不多, 只不过算和而且正向算
代码
class Solution {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int [][] square = new int[m][n];
square[0][0] = grid[0][0]; //思想
for(int i = 1; i < m; i++) {
square[i][0] = square[i-1][0]+grid[i][0]; //思想, 注意第一个是square
}
for(int j = 1; j < n; j++) {
square[0][j] = square[0][j-1]+grid[0][j];
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
square[i][j] = Math.min(square[i-1][j],square[i][j-1])+grid[i][j];
}
}
return square[m-1][n-1];
}
}
复杂度
- 时间: $O(m*n)$
- 空间: $O(m*n)$
动态规划*
思路
可以不建新数组, 直接在原数组修改
复杂度
- 时间: $O(M*N)$
- 空间: $O(1)$
75. 颜色分类
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
进阶:
- 你可以不使用代码库中的排序函数来解决这道题吗?
- 你能想出一个仅使用常数空间的一趟扫描算法吗?
桶排序思想(self
思路
扫描第一遍记录各个数字数目, 第二遍置数
复杂度
- 时间: $O(N)$
- 空间: $o(1)$
双指针*
思路
官方题解方法三.
用两个指针p1,p2来指代0和2要替换的位置, 扫描, 如果发现0的话与p1位置交换, 如果发现2的话与p2位置交换, 但是要注意, 无论是交换0还是2, 交换后的结果都有可能是三种(0和2), 这时候不能前进, 而是要将再进行交换直到不是自己.这两个做1个就行了.
代码
class Solution {
public void sortColors(int[] nums) {
int p1 = 0; //用来指示1的下次交换
int p2 = nums.length-1; //用来指示2的下次交换
for (int i = 0; i <= p2; ++i) { //思想, 注意终止条件.
if(nums[i] == 0) {
int t = nums[i];
nums[i] = nums[p1];
nums[p1] = t;
p1++;
}else if (nums[i] == 2){
int t = nums[i];
nums[i] = nums[p2];
nums[p2] = t;
p2--;
i--; //思想,如果是2的话替换之后可能是0, 可能是1, 也可能是2 所以要转变为这个位置不是2为止, 也就是其他两种情况
}else{
continue;
}
}
return;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
回溯(self
思路
回溯模板, 不用标记数组
代码
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> collections = new ArrayList<>();
List<Integer> collection = new ArrayList<>();
List<Integer> item = new ArrayList<>();
collections.add(item); //空集
dfs(collections, collection, nums.length, 0, nums);
return collections;
}
void dfs(List<List<Integer>> collections, List<Integer> collection, int depth, int index, int []nums) {
if (index == depth) {
return;
}
for(int i = index; i < depth; i++){
collection.add(nums[i]);
collections.add(new ArrayList<Integer>(collection)); //思想
dfs(collections, collection, depth, i+1, nums);
collection.remove(collection.size()-1);
}
}
}
复杂度
- 时间: $$
- 空间: $$
动态规划(self
思路
[1,2,3]的子集可以由[1,2]的子集得到
代码
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> collections = new ArrayList<>();
collections.add(new ArrayList<>()); //空集
List<Integer> temp_item = new ArrayList<>();
temp_item.add(nums[0]);
collections.add(temp_item);
for (int i = 1; i < nums.length; i++) {
int length = collections.size();
for(int j = 0; j < length; j++) {
List<Integer> new_item = new ArrayList<>(collections.get(j));
new_item.add(nums[i]);
collections.add(new_item);
}
}
return collections;
}
}
复杂度
- 时间: $O(2^N)$
- 空间: $O(2^N)$结果的空间
位运算
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
回溯
思路
我觉得很重要的一点是, 主函数要干什么, 辅助函数要干什么.
主函数: 遍历棋盘, 使用辅助函数判断是否该位置可以得到正确答案.
辅助函数:
如果是倒数第一位, 则直接返回最后一位与当前棋盘的判别, 这样是必要的, 一个是剪掉枝, 另一个最重要的是, 我们的辅助函数默认(i,j)是合法的, 如果判断最后一位与字符串的长度的话, (i, j)必然不合法.就会出现
[[a]] a这样的样例是false的结果
如果当前棋盘子和字符相同的话, 继续试探合法的棋子与下一个字符.
如果周围4个都不正常的话, 回退本棋子, 并且返回假.
代码
class Solution {
public boolean exist(char[][] board, String word) {
List<Boolean> result = new ArrayList<>();
boolean[][] board_flag = new boolean[board.length][board[0].length];
boolean flag = false;
for (int i = 0 ; i < board.length; i ++) {
for (int j = 0; j < board[0].length; j++) {
flag = exist_help(i, j, 0, board, board_flag, word);
if (flag == true) return true;
}
}
return false;
}
boolean exist_help(int i, int j, int k, char[][] board, boolean [][] board_flag, String word) {
if(k==word.length()-1) { //思想, 不能用k==word.length() return true;
return board[i][j] == word.charAt(k);
}
if (board[i][j]==word.charAt(k)) {
board_flag[i][j] = true;
if(inArea(i, j+1, board)&&!board_flag[i][j+1]) {
if (exist_help(i, j+1, k+1, board, board_flag, word)) return true;
}
if(inArea(i, j-1, board)&&!board_flag[i][j-1]) {
if( exist_help(i, j-1, k+1, board, board_flag, word)) return true;
}
if(inArea(i-1, j, board)&&!board_flag[i-1][j]) {
if( exist_help(i-1, j, k+1, board, board_flag, word)) return true;
}
if(inArea(i+1, j, board)&&!board_flag[i+1][j]) {
if( exist_help(i+1, j, k+1, board, board_flag, word)) return true;
}
board_flag[i][j] = false;
}
return false;
}
boolean inArea(int i, int j, char[][]board) {
if (i >= 0 && j >= 0 && i < board.length && j < board[0].length) {
return true;
}else {
return false;
}
}
}
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
动态规划(self
思路
可以分解为子问题, 1节点为1, 2节点为2, 3为5个节点, 然后
4可以求解:
以1为中心, 左0右3
以2为中心, 左1右2
以3为中心, 左2右1
以4为中心, 左1右3
然后左边和右边数量是相乘的关系(组合), 我第一次写为了相加.
结题思路:假设n个节点存在二叉排序树的个数是G(n),1为根节点,2为根节点,…,n为根节点,当1为根节点时,其左子树节点个数为0,右子树节点个数为n-1,同理当2为根节点时,其左子树节点个数为1,右子树节点为n-2,所以可得G(n) = G(0)G(n-1)+G(1)(n-2)+…+G(n-1)*G(0)
-评论
代码
class Solution {
public int numTrees(int n) {
int[] tree_num = new int[20];
tree_num[0] = 1;
tree_num[1] = 1;
tree_num[2] = 2;
tree_num[3] = 5;
for (int i = 4; i <= n; i++) {
for (int j = 1; j <= i; j++) {
tree_num[i]+=tree_num[j-1]*tree_num[i-j];
}
}
return tree_num[n];
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(1)$
105. 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
递归构造(self
思路
前序的第一个节点可以将中序划分为两部分, 有一个细节是, 我刚开始划分为两部分, 然后分别在递归函数里面传递两部分的首位位置s1, e1, s2, e2, 但是这样数据比较多, 而且边界不容易界定, 所以改成了传递每个部分的首位置和元素的个数, 这样少了一个计算的参数, 不容易出错.
代码
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildTreeHelp(preorder,0,inorder,0,preorder.length);
}
public TreeNode buildTreeHelp(int [] preorder, int s1, int[] inorder, int s2, int count) {
if(count==0) { //思想, 一定要注意终止条件
return null;
}
TreeNode new_node = new TreeNode(preorder[s1]);
int index = 0;
int left_num = 0; //左侧元素的个数
int right_num = 0; //右侧元素的个数, 用于确定
for (int i = s2; i < s2+count; i++) {
if(inorder[i] == preorder[s1]) {
index = i;
left_num = i - s2;
right_num = count-1-left_num;
}
}
new_node.left = buildTreeHelp(preorder, s1+1, inorder, s2, left_num);
new_node.right = buildTreeHelp(preorder, s1+left_num+1, inorder, index+1, right_num);
return new_node;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
114. 二叉树展开为链表
给你二叉树的根结点 root ,请你将它展开为一个单链表:
展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。
展开后的单链表应该与二叉树 先序遍历 顺序相同。
递归原地算法(self
思路
分各种情况讨论而已.
代码
class Solution {
public void flatten(TreeNode root) {
if (root == null) {
return;
}
else if (root.left == null && root.right == null) {
return;
}else if (root.left == null && root.right != null) {
flatten(root.right);
return;
}else if (root.left!=null && root.right == null) {
flatten(root.left);
root.right = root.left;
root.left = null;
return;
}else {
flatten(root.right);
flatten(root.left);
TreeNode temp_left = root.left;
TreeNode temp_node = root.left;
while(temp_node.right!=null) {
temp_node = temp_node.right;
}
temp_node.right = root.right;
root.right= temp_left;
root.left = null;
return;
}
}
}
代码
我的递归写复杂了
class Solution {
public void flatten(TreeNode root) {
if(root == null)
return;
// 拉直左子树
flatten(root.left);
// 拉直右子树
flatten(root.right);
// 将左子树末端连接右子树根
if(root.left !=null){
TreeNode p = root.left;
while (p.right != null)
p = p.right;
p.right = root.right;
root.right = root.left; // 右子树接到左子树
}
// 左子树置为null
root.left = null;
}
}
作者:zhy-20
链接:https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/solution/di-gui-er-cha-shu-zhan-kai-wei-lian-biao-jg0j/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
前序遍历再构造*
思路
用List存储前序遍历结果, 再根据前序遍历结果, 但是这种方法不是原地方法
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
去重排序计数(self
思路
去重排序计数
但是排序就是O(NlogN)了
代码
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
for(int item:nums){
set.add(item);
}
int size = set.size();
int count = 0;
int[] new_nums = new int[size];
for(Integer item:set) {
new_nums[count++] = item;
}
Arrays.sort(new_nums);
if(new_nums.length==0) return 0;
int max_length = 1;
int length = 1;
for (int i = 0; i < new_nums.length-1; i++) {
if(new_nums[i+1] == new_nums[i]+1) {
length++;
max_length = Math.max(max_length, length);
}else {
length = 1;
}
}
return max_length;
}
}
复杂度
- 时间: $O(NLogN)$
- 空间: $O(N)$
Hash*
思路
将数据存储到哈希表中, 再遍历, 如果某个数是开头(没有它的前一个数), 则进内循环得到以它为首的序列的长度, 否则不进内循环.
代码
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
for(int item:nums){
set.add(item);
}
int max_length = 0;
int length = 1;
for(int item:set) {
if (!set.contains(item-1)) {
int next_item = item+1;
while(set.contains(next_item)) {
next_item++;
length++;
}
max_length = Math.max(length, max_length);
}
length = 1;
}
return max_length;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
136. 只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
位运算*
思路
位运算, 异或: 相异为1, 相同为0.
Java提供的位运算符有:左移( << )、右移( >> ) 、无符号右移( >>> ) 、位与( & ) 、位或( | )、位非( ~ )、位异或( ^ ),除了位非( ~ )是一元操作符外,其它的都是二元操作符。
代码
class Solution {
public int singleNumber(int[] nums) {
int result = 0;
for (int i = 0; i < nums.length; i++) {
result = result ^ nums[i];
}
return result;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
139. 单词拆分⏰
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
示例 2:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出: false
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅有小写英文字母组成
wordDict 中的所有字符串 互不相同
用set存储后递归(self, 没解决
思路
用set存储字典, 然后递归判断, 为了加快速度, 使用字典中字词的最短长度和最长长度.
但是下面的样例会超出时间限制.
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"]
因为是递归遍历, 而且aaaaaaa与[a, aa, aaa]有太多次匹配和递归了.
如果有优化的话, 就是将字典中的词典,只存储最小的”字”, 比如[a, aa]只存储[a], 纸样的话下面的代码可以改造为
return wordBreakHelp(s.substring(i), wordDictSet, shortest, longest);
代码
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
int shortest = 21;
int longest = 0;
Set<String> wordDictSet = new HashSet<String>();
for (int i = 0; i < wordDict.size(); i++) {
wordDictSet.add(wordDict.get(i));
shortest = Math.min(wordDict.get(i).length(), shortest);
longest = Math.max(wordDict.get(i).length(), longest);
}
return wordBreakHelp(s, wordDictSet, shortest, longest);
}
public boolean wordBreakHelp(String s, Set<String> wordDictSet, int shortest, int longest) {
boolean flag = false;
if(s.length() == 0) return true;
for(int i = shortest; i <= longest; i++) {
if (s.length() < i) return false;
if (wordDictSet.contains(s.substring(0,i))) {
flag = wordBreakHelp(s.substring(i), wordDictSet, shortest, longest);
if(flag) return true;
}
}
return false;
}
}
复杂度
- 时间: $$
- 空间: $$
思想2名称*
思路
描述
代码
复杂度
- 时间: $$
- 空间: $$
142. 环形链表 II
给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表。
快慢指针+一二两次相遇
思路
==第一次相遇的节点 和 头结点 同时移动, 下次相同的节点就是入口==
总结关键点(注意a是除环外的长度(也就是起始点距离进入环节点的距离),b是环的长度, n是未知数)
- 1.第一次相遇,slow = nb(是由fast=2slow, fast = slow+nb推出的)
- 2.a+nb = 入口点
- 3.slow再走a = 入口 = head走到入口 = a
- 4.由3得出,起始点(head) + a = 第一次相遇位置(nb) + a
- 5.a不是显性的求出来的, 只需要同时移动起始点和第一次相遇位置即可
感觉就是数学公式推导+逻辑结合的一道题
代码
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(true) {
if(slow == null || fast == null || fast.next == null) return null; //无环
slow = slow.next;
fast = fast.next.next;
if (slow == fast) break; //第一次相遇
}
// f = 2s
// f = s+nb 快慢指针相遇时走的步数为s的步数+n圈环的步数
// s = nb 快慢指针相遇时s的步数由前两式子得到为nb
// 将f置为0, s=nb, 快慢指针再次向前移动, 两者相遇时节点为环的入口.
ListNode temp = head;
while(temp != slow) { //然后起始点+a = nb + a, 而nb + a就是入口点也就是答案
temp = temp.next;
slow = slow.next;
}
return temp;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
修改链表
思路
遍历链表, 将链表的每个节点.next都赋值为temp, 这样就把节点一个一个拆开了(不符合题意), 遇到环的时候就是.next==temp的时候.
146. LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
- LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
- int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
- void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
自制双向链表(self
思路
代码
class BiLinkedNode{
public BiLinkedNode previous;
public BiLinkedNode next;
public int key;
public int val;
BiLinkedNode(){
previous = null;
next = null;
val = -1;
}
BiLinkedNode(int key, int val){
previous = null;
next = null;
this.key = key;
this.val = val;
}
}
class LRUCache {
private int capacity;
private int count;
private BiLinkedNode head;
private BiLinkedNode tail;
private Map<Integer, BiLinkedNode> m;
public LRUCache(int capacity) {
this.capacity = capacity;
this.count = 0;
this.m = new HashMap<>();
this.head = new BiLinkedNode();
this.tail = new BiLinkedNode();
head.next = tail; //思想,头节点是假节点.
tail.previous = head; //思想,注意tail是单独的tail
}
public int get(int key) {
if(m.containsKey(key)) {
BiLinkedNode temp = new BiLinkedNode(key, m.get(key).val);
deleteNode(m.get(key));
insertLast(temp);
m.remove(key);
m.put(key, temp);
return m.get(key).val;
}
else return -1;
}
public void put(int key, int value) {
if (m.containsKey(key)==true) {
deleteNode(m.get(key));
m.remove(key);
BiLinkedNode temp = new BiLinkedNode(key, value);
m.put(key, temp);
insertLast(temp);
}
else {
if (count==capacity) {
BiLinkedNode temp = new BiLinkedNode(key, value);
System.out.println("key:"+key+" remove"+head.next.val);
m.remove(head.next.key); //这里应该是移除head.next.val对应的key
deleteFirst();
m.put(key, temp);
insertLast(temp);
}else {
BiLinkedNode temp = new BiLinkedNode(key, value);
insertLast(temp);
m.put(key, temp);
count+=1;
}
}
}
public void deleteFirst() { //语法, 其实可以与下面的合并
head.next = head.next.next;
head.next.previous = head;
return;
}
public void deleteNode(BiLinkedNode temp) {
temp.previous.next = temp.next;
temp.next.previous = temp.previous;
return;
}
public void insertLast(BiLinkedNode temp) {
tail.previous.next = temp;
temp.previous = tail.previous;
temp.next = tail;
tail.previous = temp;
return;
}
public void printList() {
BiLinkedNode node= head.next;
while(node !=null) {
System.out.print(node.val+" ");
node = node.next;
}
System.out.println();
return;
}
}
我构造了太多的节点了, 没有弄好数据结构和面向对象化数据结构,导致代码重用性不高, 开销大, 但至少AC了
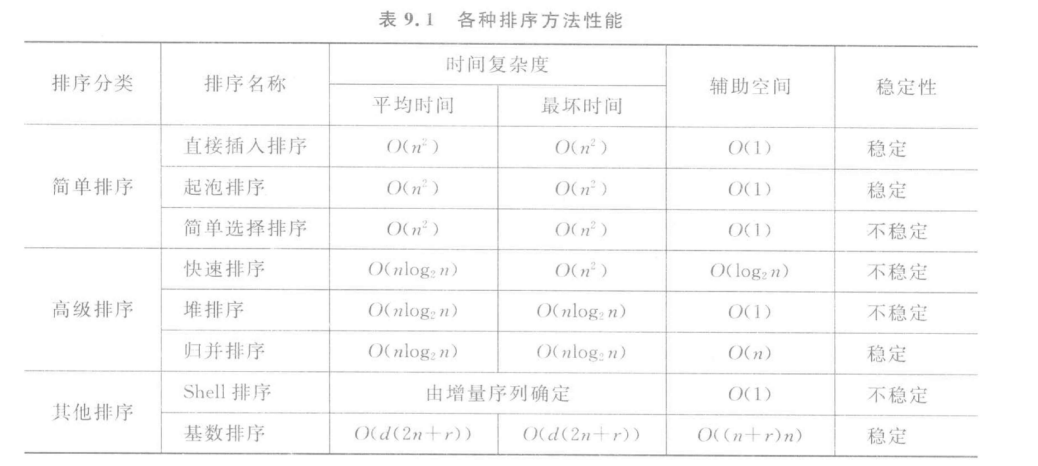
148. 排序链表
给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
输入:head = [4,2,1,3](以链表形式存在)
输出:[1,2,3,4]
进阶:你可以在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
list存储快排后再赋值(self
思路
list存储快排后再赋值给链表
代码
class Solution {
public ListNode sortList(ListNode head) {
List<Integer> data = new ArrayList<>();
ListNode p = head;
while(p != null) {
data.add(p.val);
p = p.next;
}
Collections.sort(data);
p = head;
for(int i = 0; i < data.size(); i++) {
p.val = data.get(i);
p = p.next;
}
return head;
}
}
复杂度
- 时间: $O(NLogN)$
- 空间: $O(N)$
归并(slef*
思路
平均时间为O(NlogN)并且辅助空间为O(1)的只能是归并(对链表排序的最佳方案).
代码
class Solution {
public ListNode sortList(ListNode head) {
int length = 0;
ListNode point = head;
while(point != null) {
length++;
point = point.next;
}
return sortListHelp(head, length);
}
public ListNode sortListHelp(ListNode head, int length) {
if (length == 1||length == 0) {
return head;
}
ListNode first_point = head;
ListNode another_head = head;
for(int i = 0; i < length - length/2; i++) {
if (i == length-length/2-1) {
another_head = first_point.next;
first_point.next = null;
}else{
first_point = first_point.next;
}
}
ListNode first_head = sortListHelp(head, length - length/2);
ListNode second_head = sortListHelp(another_head, length/2);
ListNode new_head = new ListNode();
ListNode point = new_head;
while(first_head != null && second_head != null) {
if (first_head.val < second_head.val) {
point.next = first_head;
first_head = first_head.next;
point = point.next;
}else {
point.next = second_head;
second_head = second_head.next;
point = point.next;
}
}
while(first_head!=null) {
point.next = first_head;
first_head = first_head.next;
point = point.next;
//以上可以简写为point.next = first_head即可.
}
while(second_head!=null){
point.next = second_head;
second_head = second_head.next;
point = point.next;
//以上可以简写为point.next = second_head即可.
}
point.next = null;
return new_head.next;
}
}
复杂度
- 时间: $O(NlogN)$
- 空间: $O(1)$
152. 乘积最大子数组
给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
子数组 是数组的连续子序列。
以0分割后双向遍历遇到负数个数为奇数时最后一个奇数停止
思路
[1, 2, -3, -4, -5] 的最大值是[1, 2, -3, -4]和[-4, -5]中的一个.
[1, 2, 0, 3, 4]的最大值是[1, 2]和[3, 4]中的一个.
代码
class Solution {
public int maxProduct(int[] nums) {
int max = -11; //结果,-11因为最小是-10
int s = 0; //开始下标预赋值
int e = nums.length-1; //结束下标预赋值
List<List<Integer>> zero_index = new ArrayList<>();
int zero_count = 0;
// 求得以0为分割的区间下标起始点和终止点
for (int i = 0; i < nums.length; i++) {
List<Integer> pair = new ArrayList<>();
if(nums[i] == 0) {
pair.add(s);
pair.add(i-1);
zero_index.add(pair);
s = i+1;
zero_count++;
}
if(i == nums.length-1){
if(nums[i] == 0){
break;
}else{
pair.add(s);
pair.add(i);
zero_index.add(pair);
}
}
}
//以0左分割
for (int i = 0; i < zero_index.size(); i++) {
int product = maxProductHelp(nums, zero_index.get(i).get(0), zero_index.get(i).get(1));
max = Math.max(max, product);
}
//因为0也是子序列, 所以以防[-2, 0]这种样例
if (zero_count > 0) {
return Math.max(max, 0);
}
return max;
}
public int maxProductHelp(int [] nums, int s, int e) {
int count = 0; //负数的个数
//统计负数的个数
for (int i = s; i <= e; i++) {
if (nums[i] < 0) {
count++;
}
}
if(e <= s) return nums[s]; //如果是一个数则直接返回
if(count%2 == 0) { //如果负数时偶数则直接乘积返回
int result = 1;
for(int i = s; i <= e; i++) {
result = result * nums[i];
}
return result;
}
//要么是从左往右相乘遇到最后一个负数停止的积
//要么是从右往左相乘遇到最后一个负数停止的积
int count1 = 0;
int product1 = 1;
int count2 = 0;
int product2 = 1;
for(int i = s; i <= e; i++) {
if(nums[i] < 0) count1++;
if(count1 == count) {
break;
}
product1 = product1 * nums[i];
}
for(int i = e; i >= s; i--) {
if(nums[i] < 0) count2++;
if(count2 == count){
break;
}
product2 = product2 * nums[i];
}
return Math.max(product1, product2);
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
动态规划⏰
思路
动态规划方程
maxF[i] = Math.max(Math.max(maxF[i-1]*nums[i], minF[i-1]*nums[i]), nums[i]);
minF[i] = Math.min(Math.min(maxF[i-1]*nums[i], minF[i-1]*nums[i]), nums[i]);
代码
class Solution {
public int maxProduct(int[] nums) {
int length = nums.length;
int max = nums[0];
int[] maxF = new int[length];
int[] minF = new int[length];
if(length == 1) return nums[0];
System.arraycopy(nums, 0, maxF, 0, length);
System.arraycopy(nums, 0, minF, 0, length);
for(int i = 1; i < length; i++) {
maxF[i] = Math.max(Math.max(maxF[i-1]*nums[i], minF[i-1]*nums[i]), nums[i]);
minF[i] = Math.min(Math.min(maxF[i-1]*nums[i], minF[i-1]*nums[i]), nums[i]);
}
for(int i = 0; i < length; i++) {
max = Math.max(maxF[i], max);
}
return max;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
155. 最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
实现 MinStack 类:
MinStack() 初始化堆栈对象。
void push(int val) 将元素val推入堆栈。
void pop() 删除堆栈顶部的元素。
int top() 获取堆栈顶部的元素。
int getMin() 获取堆栈中的最小元素。
一个数字栈一个最小数字栈(self
思路
本来想用优先队列存储最小元素的, 但是发现无法以O(1)在pop的时候也删除最小元素, 所以想到了两个栈, 以前数据结构时作过.
代码
class MinStack {
private List<Integer> minStack;
private int count;
private List<Integer> numStack;
public MinStack() {
numStack = new ArrayList<>();
minStack = new ArrayList<>();
count = 0;
}
public void push(int val) {
numStack.add(val);
if (count == 0) {
minStack.add(val);
}else {
int min = this.getMin();
if(min < val) {
minStack.add(min);
}else{
minStack.add(val);
}
}
count++;
}
public void pop() {
numStack.remove(count-1);
minStack.remove(count-1);
count--;
}
public int top() {
return numStack.get(count-1);
}
public int getMin() {
return minStack.get(count-1);
}
}
复杂度
- 时间: $$
- 空间: $$
自定义pair链表存储*
思路
pair存储数字和对应的最小数字
代码
class MinStack {
private Node head;
public void push(int x) {
if(head == null)
head = new Node(x, x);
else
head = new Node(x, Math.min(x, head.min), head);
}
public void pop() {
head = head.next;
}
public int top() {
return head.val;
}
public int getMin() {
return head.min;
}
private class Node {
int val;
int min;
Node next;
private Node(int val, int min) {
this(val, min, null);
}
private Node(int val, int min, Node next) {
this.val = val;
this.min = min;
this.next = next;
}
}
}
160. 相交链表
给你两个单链表的头节点 headA 和 headB ,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回 null 。
指针法(self
思路
让长的链表先移动Math.abs(LengthA-LengB), 然后两个一起移动, 移动到末尾时还没有相等则为null, 否则返回相同的节点.
代码
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lengthA = getLength(headA);
int lengthB = getLength(headB);
ListNode longHead = lengthA > lengthB ? headA:headB;
ListNode shortHead = lengthA > lengthB ? headB:headA;
ListNode newLongHead = move(longHead, Math.abs(lengthA-lengthB));
for (int i = 0; i < Math.min(lengthA, lengthB); i++) {
if(newLongHead == null || shortHead ==null) return null;
else if (newLongHead == shortHead) return newLongHead;
newLongHead = move(newLongHead, 1);
shortHead = move(shortHead, 1);
}
return null;
}
public ListNode move(ListNode head, int step){
ListNode node = head;
for(int i = 0; i < step; i++) {
node = node.next;
}
return node;
}
public int getLength(ListNode head){
int length = 0;
ListNode node = head;
while(node != null){
length++;
node = node.next;
}
return length;
}
public void printHead(ListNode head) {
ListNode node = head;
while(node != null) {
System.out.print(node.val);
node = node.next;
}
System.out.println();
}
}
复杂度
- 时间: $O(M+N)$
- 空间: $O(1)$
双指针优雅永不过时*
思路
让两个指针移动, 谁移动到末尾就指向另一个链表的头部, 这样的话等两个指针各移动一次到末尾之后就长度相等了, 抹平了不相等的那一部分.
代码
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA = headA, pB = headB;
while (pA != pB) {
pA = pA == null ? headB : pA.next;
pB = pB == null ? headA : pB.next;
}
return pA;
}
}
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/intersection-of-two-linked-lists/solution/xiang-jiao-lian-biao-by-leetcode-solutio-a8jn/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
复杂度
- 时间: $O(M+N)$
- 空间: $O(1)$
169. 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
摩尔投票
思路
遇到相同的计数+1, 否则计数-1, 如果计数为0则换个数字.
代码
class Solution {
public int majorityElement(int[] nums) {
int count = 0;
int num = nums[0];
for(int i = 0; i < nums.length; i++){
if(count == 0) {
num = nums[i];
count++;
}else {
if (nums[i] != num) {
count--;
}else{
count++;
}
}
}
return num;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
200. 岛屿数量
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
深度遍历(self
思路
用标记数组先标记海洋为访问过, 然后遍历每一个陆地, 将陆地的连片岛屿进行标记为访问过.
遍历每一个陆地, 如果没有访问过就数字+1
代码
class Solution {
private int[][] bias = new int[][]{{-1,0},{+1,0},{0,-1},{0,+1}};
public int numIslands(char[][] grid) {
boolean flag = false;
int[][] visited = new int[grid.length][grid[0].length];
int num = 0;
for(int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if(grid[i][j] == '0') {
visited[i][j] = 1;
}
}
}
for(int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (visited[i][j] == 0) {
num++;
numIslandsHelp(grid, visited, i, j);
}
}
}
return num;
}
public void numIslandsHelp(char[][] grid, int[][]visited, int m, int n){
if(m < 0 || m >= grid.length || n < 0 || n >= grid[0].length) {
return;
}
if(visited[m][n] == 1) {
return;
}
visited[m][n] = 1;
for(int i = 0;i < 4; i++) {
int x = m+bias[i][0];
int y = n+bias[i][1];
numIslandsHelp(grid, visited, x, y);
}
return;
}
}
复杂度
- 时间: $O(M*N)$
- 空间: $O(M*N)$
208. 实现 Trie (前缀树)
Trie(发音类似 “try”)或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
Trie
思路
前缀树的节点是这样的:
private class TrieNode { //语法
boolean isKey;
TrieNode[] children;
TrieNode(){
isKey = false;
children = new TrieNode[26]; //思想
}
}
如果一个孩子不存在, 是这样判断的(也就是TrieNode[]的默认值是null):
if(node.children[pos]==null)
代码
class Trie {
private class TrieNode { //语法
boolean isKey;
TrieNode[] children;
TrieNode(){
isKey = false;
children = new TrieNode[26]; //思想
}
}
private TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
int pos = word.charAt(i)-'a';
if(node.children[pos]==null){ //思想
TrieNode new_children = new TrieNode();
node.children[pos] = new_children;
node = node.children[pos]; //思想,
}
else{
node = node.children[pos];
}
}
node.isKey = true;
return;
}
public boolean search(String word) {
TrieNode node = root;
for (int i = 0; i < word.length(); i++) {
int pos = word.charAt(i)-'a';
if(node.children[pos]==null){
return false;
}else{
node = node.children[pos];
}
}
return node.isKey;
}
public boolean startsWith(String prefix) {
TrieNode node = root;
for (int i = 0; i < prefix.length(); i++) {
int pos = prefix.charAt(i)-'a';
if(node.children[pos]==null){
return false;
}else{
node = node.children[pos];
}
}
return true;
}
}
215. 数组中的第K个最大元素⏰
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
调用库函数(self
代码
class Solution {
public int findKthLargest(int[] nums, int k) {
Arrays.sort(nums); //语法
return nums[nums.length-k];
}
}
复杂度
- 时间: $$
- 空间: $$
思想2名称*
思路
描述
代码
复杂度
- 时间: $$
- 空间: $$
221. 最大正方形
在一个由 '0' 和 '1' 组成的二维矩阵内,找到只包含 '1' 的最大正方形,并返回其面积。
动态规划(self
思路
$dp[i][j]$代表该位置为正方形右下角的最大边长.
$$
dp[i][j] = 0 if(matrix[i][j] == 0)\
dp[i][j] = 1+[1,2,m,..dp[i-1][j-1]]中最大的m使得matrix[i-(1..m)][j]和matrix[i][j-(1..m)]都是1.
$$
代码
class Solution {
public int maximalSquare(char[][] matrix) {
int rowNum = matrix.length;
int colNum = matrix[0].length;
int[][] flag = new int[rowNum][colNum];
int max = 0; //最大边长
for(int i = 0; i < rowNum; i++) {
for(int j = 0; j < colNum; j++) {
flag[i][j] = matrix[i][j]-'0';
}
}
for(int i = 1; i < rowNum; i++) {
for(int j = 1; j < colNum; j++) {
int last = flag[i-1][j-1]; //以左上角的那个元素为正方形右下角的最大边长
for(int k = last; k >= 1; k--) {
//从高往低刷
boolean tag = true; //i行j列的元素是否都>0(表示可以是边长)
for(int m = 1; m <= k; m++) {
tag = tag && flag[i][j-m]>0?true:false;
tag = tag && flag[i-m][j]>0?true:false;
}
if(tag == true && flag[i][j] == 1) {
flag[i][j] += k;
break; //如果已经组成正方形则break,防止正方形边长缩小
}
}
}
}
for(int i = 0; i < rowNum; i++) {
for (int j = 0; j < colNum; j++) {
max = Math.max(max, flag[i][j]);
}
}
return max*max;
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(N^2)$
动态规划*
思路
dp[i][j]表示以第i行第j列为右下角所能构成的最大正方形边长, 则递推式为: dp[i][j] = 1 + min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]);
234. 回文链表
给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。
折半反转对比(self
思路
折半反转对比
代码
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
int length = 0;
ListNode node = head;
ListNode head2;
ListNode new_head = new ListNode();
//求链表长度
while(node!=null) {
length++;
node = node.next;
}
node = head;
//将链表对半
for(int i = 0; i < (length+1)/2-1; i++) {
node = node.next;
}
head2 = node.next;
node.next = null;
//转置链表
while(head2 != null) {
ListNode temp = head2.next;
head2.next = new_head.next;
new_head.next = head2;
head2 = temp;
}
new_head = new_head.next;
//判断饭转后的链表的一半是否和另一半相同
for(int i = 0; i < length/2; i++) {
if(head.val == new_head.val) {
head = head.next;
new_head = new_head.next;
continue;
}
else return false;
}
return true;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
快慢指针*(⏰
思路
描述
代码
复杂度
- 时间: $$
- 空间: $$
236. 二叉树的最近公共祖先(LCA)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。
后序遍历
思路
递归函数:
- 返回值: 返回root节点下最近的含有p或者q的节点
- 终止条件:
- 如果root是p或者q返回root, 否则(root==null或者其他情况)返回null
- 后序遍历子树
- 如果左孩子和右孩子中都有p或者q的父节点的话, 返回root(因为是后序遍历, 自底向上遍历, 所以第一次返回的必然是最近公共祖先), 否则只返回含有p或者q的节点
代码
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//递归函数:如果root是p或q的最近父节点,返回root,否则返回null
if(root == p || root == q || root == null) return root;
TreeNode left_father = lowestCommonAncestor(root.left, p, q);
TreeNode right_father = lowestCommonAncestor(root.right, p, q);
//想法, 后序遍历
if (left_father!= null && right_father != null) {
//如果左右孩子都有p或者q, 则root是最近父节点
return root;
}else if (left_father != null) {
//如果左孩子下面有节点是p或q的父节点(此时右孩子不是p或者q的父节点),返回该节点
return left_father;
}else if (right_father != null) {
return right_father;
}else{
return null;
}
}
}
复杂度
- 时间: $O(N)$(每个节点被访问一次)
- 空间: $O(N)$(最差情况下为一条单链)
238. 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组不被视为额外空间。
左累乘右累乘再相乘
思路
用两个数组存储某位的左累乘和右累乘的结果, 比如
[1, 2, 3, 4]
[1 ,1, 1*2, 1*2*3]
[2*3*4,3*4, 4, 1]
而在计算下面这两个数组的时候是可以优化为O(1)的, 因为是累乘.
注意:
- O(N)算法可以扫描多遍
- O(1)算法用累乘
代码
class Solution {
public int[] productExceptSelf(int[] nums) {
int[] result = new int[nums.length];
int p = 1; //存储某个数左边的连乘结果
int q = 1; //存储某个数右乘的连乘结果
result[0] = 1;
for(int i = 1; i < nums.length; i++) {
p = p*nums[i-1];
result[i] = p;
}
for(int i = nums.length-2; i >= 0; i--) {
q = q*nums[i+1];
result[i] = result[i] * q;
}
return result;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
暴力遍历
思路
逐个遍历比较
代码
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
for (int i = 0; i < matrix.length; i++) {
for(int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == target) return true;
}
}
return false;
}
}
复杂度
- 时间: $O(M*N)$
- 空间: $O(1)$
对每行二分查找
思路
对每行使用二分查找
代码
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
for (int[]nums:matrix){
int result = search(nums, target);
if (result != -1) return true;
}
return false;
}
public int search(int[] nums, int target){
int low = 0;
int high = nums.length-1;
while(low <= high) {
int mid = (high-low)/2+low;
int num = nums[mid];
if (num == target){
return mid;
}else if (num> target){
high = mid-1;
}else{
low = mid + 1;
}
}
return -1;
}
}
复杂度
- 时间: $O(N*log^N)$
- 空间: $O(1)$
279. 完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
动态规划
思路
动态规划方程:
$$
f[i] = 1 + min(f_{j=1}^\sqrt[2]i[i-j*j])
$$
含义是:
正如i的完全平方数的最少数量等于1+比它小的能组成它的数字的完全平方数的最小数量.
代码
class Solution {
public int numSquares(int n) {
int []f = new int[n+1];
f[0] = 0;
for(int i = 1; i <= n; i++){
int min = Integer.MAX_VALUE;
for(int j = 1; j * j <= i; j++){
min = Math.min(min, f[i-j*j]); //思想
}
f[i] = min+1;
}
return f[n];
}
}
复杂度
- 时间: $O(N*\sqrt[2]{N}$
- 空间: $O(N)$
数学法
思路
四平方和定理: 一个数最多能表示为4个平方数之和, 如果恰好为4个平方数之和, 那必然满足$n=4^i+(8j+7)$.
那么一个数的平方数只有以下可能:
- 4 : 满足$n=4^i+(8j+7)$.
- 1: 满足$n=i*i$
- 2: 满足$n=ii + jj$
- 3: 不满足以上条件
代码
class Solution {
public int numSquares(int n) {
if(satisfy4(n)) return 4;
else if(satisfy1(n)) return 1;
for(int i = 0; i*i<n; i++){
if(satisfy1(n-i*i)) return 2;
}
return 3;
}
boolean satisfy4(int n){ //思想
while(n%4==0){
n = n/4;
}
return n%8==7;
}
boolean satisfy1(int n){ //思想
int r = (int)Math.sqrt(n);
return r*r == n;
}
}
复杂度
- 时间: $O(\sqrt[2]{N})$
- 空间: $O(1)$
283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
将非0覆盖到数组前面后面赋值0(self
思路
第一次遍历计算0的个数, 然后第二次遍历将非0元素覆盖到前面, 后面再赋值count个0到数组后面
覆盖法的优点是每个都要赋值一次,但是原本结果是0的位置全部要写一次。 交换法虽然每次代价是赋值2次(a=b;b=0;),但是后面都是0的位置可以不用再操作了。
代码
class Solution {
public void moveZeroes(int[] nums) {
int start = 0;
int count = 0;
//计算0元素个数
for(int i = 0; i < nums.length; i++) {
if(nums[i] == 0) count++;
}
for(int i = 0; i < nums.length; i++) {
if (nums[i] != 0) nums[start++] = nums[i];
if (i >= nums.length-count) nums[i] = 0;
}
return;
}
}
复杂度
- 时间: $$
- 空间: $$
左右指针⏰
思路
代码
class Solution {
public void moveZeroes(int[] nums) {
int left = 0;
int right = 0;
while(right < nums.length) {
if (nums[right] != 0) {
int temp = nums[right];
nums[right] = nums[left];
nums[left] = temp;
left++;
}
right++;
}
return;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums ,其数字都在 [1, n] 范围内(包括 1 和 n),可知至少存在一个重复的整数。
假设 nums 只有 一个重复的整数 ,返回 这个重复的数 。
你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。
快慢指针法
思路
描述
代码
class Solution {
public int findDuplicate(int[] nums) {
int fast = 0;
int low = 0;
do{
fast = nums[fast];
fast = nums[fast];
low = nums[low];
}while(fast!=low); //思想, 先判断有无环
low = 0; //思想,将慢指针置为起始点,然后快慢再一起移动, 再相遇时就是环的入口
while(low!=fast){
low = nums[low];
fast = nums[fast];
}
return low;
}
}
复杂度
- 时间: $O(N)$「Floyd 判圈算法」时间复杂度为线性的时间复杂度。
- 空间: $O(1)$
300. 最长递增子序列
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
动态规划
思路
动态规划方程:
f[i]表示以第i个位置结尾的递增子序列的长度, 就等于扫描一遍该位置前面的f[j], 如果nums[i] > nums[j]的话, f[i] = f[j]+1之间的最大值
$$
f[i] = Math.max(f_{j=1}^{i-1}[j]+1) if(nums[i]>nums[j])
$$
代码
class Solution {
public int lengthOfLIS(int[] nums) {
int []f = new int[nums.length];
f[0] = 1;
for(int i = 1; i < nums.length; i++){
f[i] = 1;
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]) {
f[i] = Math.max(f[j]+1,f[i]); //思想, 递归方程
}
}
}
int result = Integer.MIN_VALUE;
for(int i = 0; i<nums.length;i++){ //思想, 是所有中最大的那个, 并不一定是最后的那个
result = Math.max(f[i],result);
}
return result;
}
}
复杂度
- 时间: $O(N^2)$
- 空间: $O(N)$
309. 最佳买卖股票时机含冷冻期
给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
动态规划
思路
第i天有这么几种可能性f[i], f[i]记为净收益:
- 现在手上持有股票
- 这种状态只能由第i-1天持有股票或者第i-1天可以购买股票时净收益减去今天购买股票花费转化而来
- $$f[i][0] = max( f[i-1][0], f[i-1][2]-prices[i])$$
- 现在处于冷冻期
- 这种状态只能由第$$i-1$$天持有股票转化而来
- $$f[i][1] = f[i-1][1]+prices[i]$$
- 现在既不持有股票也不处于冷冻期(可以购买股票
- 这种情况由第$$i-1$$天为冷冻期或者第$$i-1天$$可以购买股票转换而来
- $$f[i][2] = Math.max(f[i-1][1], f[i-1][2])$$
代码
class Solution {
public int maxProfit(int[] prices) {
int[][] f= new int[prices.length][3];
f[0][0] = -prices[0]; //持有股票的净收益
f[0][1] = 0; //冷冻期的净收益
f[0][2] = 0; //可以购买股票的净收益
for(int i = 1; i < prices.length; i++){
f[i][0] = Math.max(f[i-1][0], f[i-1][2]-prices[i]);
f[i][1] = f[i-1][0]+prices[i];
f[i][2] = Math.max(f[i-1][1], f[i-1][2]);
}
return Math.max(f[prices.length-1][1],f[prices.length-1][2]);
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(N)$
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
从上往下记忆化搜索
思路
$$
F[n] = \min_{i=0…n-1}(F[n-c_i])+1
\
F[0] = 0
\
F[负数] = -1
$$
代码
class Solution {
public int coinChange(int[] coins, int amount) {
if(amount < 1) {
return 0;
}
return coinChange(coins, amount, new int[amount]);
}
private int coinChange(int[] coins, int rem, int[] f) { //返回
if(rem < 0) {
return -1; //表示组成不了
}
if(rem == 0) {
return 0; //表示恰好组成
}
if(f[rem-1] != 0) { //记忆化搜索
return f[rem-1];
}
int min = Integer.MAX_VALUE;
for(int coin:coins) {
int res = coinChange(coins, rem-coin, f);
if(res >= 0 && res < min) { //能组成并且比其他的方案需要硬币小
min = res + 1;
}
}
f[rem-1] = (min==Integer.MAX_VALUE)?-1:min;
return f[rem-1];
}
}
复杂度
- 时间: $O(Sn)$, S为状态数, n为面值数, 每个状态遍历面值计算一遍
- 空间: $O(S)$, S的数组来存储计算出来的答案
动态规划
思路
$$
F[0] = 0;
f[S] = \min_{i=0,n-1}(f[S-coin_i])+1
$$
代码
class Solution {
public int coinChange(int[] coins, int amount) {
int max = amount+1;
int []f = new int[amount+1];
Arrays.fill(f, max);
f[0] = 0;
for(int i = 1 ; i <= amount; i++) {
int min = max;
for(int j = 0; j < coins.length; j++){
int res = (i-coins[j])<0 ?max:f[i-coins[j]]+ 1;
if(res<min){
min = res;
}
}
f[i] = min;
}
if(f[amount] >= max) return -1;
else return f[amount];
}
}
复杂度
- 时间: $O(Sn)$
- 空间: $O(S)$
338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
动态规划(self
思路
动态规划方程:
$$
ans[i] = ans[i>>1]+(i%2==1)?1:0
$$
代码
class Solution {
public int[] countBits(int n) {
int[]ans = new int[n+1];
if(n < 1) return ans;
ans[0] = 0;
for(int i = 1; i <= n; i++){
int num = i;
if(i % 2 == 0){
ans[i] = ans[num>>1]; //语法
}else{
ans[i] = ans[num>>1]+1;
}
}
return ans;
}
}
复杂度
- 时间: $O(N)$
- 空间: $O(1)$
347. 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
哈希表+优先队列(堆)
思路
哈希表计数, 优先队列为小顶堆存储计数结果, 如果队列长度小于k, 则直接入队, 队列长度大于k, 出堆顶然后入队.
代码
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> m = new HashMap<Integer, Integer>();
for(int i = 0; i < nums.length; i++){
m.put(nums[i], m.getOrDefault(nums[i],0)+1);
}
//语法
PriorityQueue<int[]> queue= new PriorityQueue<int[]>(new Comparator<int[]>(){
public int compare(int[] a, int [] b){
return a[1] - b[1];
}
});
for(Map.Entry<Integer, Integer> entry : m.entrySet()){ //语法
int num = entry.getKey();
int count = entry.getValue();
if(queue.size() == k) { //思想
if(queue.peek()[1] < count){
queue.poll();
queue.offer(new int[]{num, count});
}
} else {
queue.offer(new int[]{num, count});
}
}
int []result = new int[k];
for (int i = 0; i < k; i++) {
result[i] = queue.poll()[0];
}
return result;
}
}
复杂度
- 时间: $O(Nlogk)$k为堆的节点数目
- 空间: $O(N)$
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
提示:
1 <= s.length <= 30
s 由小写英文字母、数字和方括号 '[]' 组成
s 保证是一个 有效 的输入。
s 中所有整数的取值范围为 [1, 300]
栈
思路
- 遇到
]- 弹出栈内字符直到遇到
[, 得到[前面的数字, 然后将重复的字符串再入栈
- 弹出栈内字符直到遇到
- 其他
- 入栈
代码
class Solution {
public String decodeString(String s) {
Stack<Character> stack = new Stack<>();
for(int i = 0; i < s.length(); i++) {
if(s.charAt(i) != ']') {
stack.push(s.charAt(i));
}else{
char topChar;
String str="";
while(stack.peek() != '[') {
topChar = stack.pop();
str = topChar+str;
}
stack.pop(); //弹出'['
String numString = ""; //数组为多位数
while(!stack.empty() && stack.peek() >= '0' && stack.peek() <= '9') {
topChar = stack.pop();
numString = topChar + numString;
}
int count = Integer.parseInt(numString);
for(int j = 0; j < count; j++) {
for(int k = 0; k < str.length(); k++) {
stack.push(str.charAt(k));
}
}
}
}
List<Character> resultList = new ArrayList<>(stack);
String result = "";
for(Character c:resultList) {
result+=c;
}
return result;
}
}
复杂度
- 时间: $O(S)$ S为解码后的字符串长度
- 空间: $O(S)$
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/queue-reconstruction-by-height
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。模:sob:
动态规划😭
思路
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]], 思路是每次挑选这个位置上应该存在的人
首先挑选正确答案第0个位置的人, 这个人一定是k=0并且h是最小的, 因为这个人k=0表明前面没有比它等高或更高的,
利用反证法: 假设这个人
队头的人, 那么一定存在一个比它更矮的人, 并且k=0, 但这个人不存在, 说明挑选正确.然后, 把队头挑选出来后, 其他位置的人肯定排在他的后面, 所以如果身高小于等于这个
队头话, k要减一, 然后重复第1个步骤.
1. 挑选出[5,0], 新k: [7,0],[4,3],[7,1],[6,1],[5,1], 原来k:[7,0],[4,4],[7,1],[6,1],[5,2], 此时队列内为5,0],
2. 挑选出[7,0]对应的原来[7,1],新k:[4,2],[7,0],[6,0],[5,0],原来k:[4,3],[7,1],[6,1],[5,1],此时队列内为[5,0],[7,1]
3. 挑选出新k队列的[5,0]对应的原来[5,2],新k:[4,1],[7,0],[6,0]此时队列为[5,0],[7,1],[5,2]
4. 挑选出[6,0]对应的原来[6,1], 新k: [4,0],[7,0] 此时队列为[5,0],[7,1],[5,2], [6,1]
5. 挑选出[4,0]对应的原来[4,4], 新k:[7,0], 此时队列为[5,0],[7,1],[5,2], [6,1], [4,4]
6. 挑选出[7,0]对应的原来[7,1], 此时队列为[5,0],[7,1],[5,2], [6,1], [4,4],[7,1]
代码
\\语法, 以后搜索\\语法可以学习语法
\\思想, 学习思想
h逆序k顺序排序+插队*
思路
为什么要按照身高降序和k升序排列呢? 举个例子,[7, 0] [7, 1] [6, 1] [5, 0] [5, 2] [4, 4],
- 迎面走来了最高之人,身高为 7,他往队伍第 0 个位置一站,由于目前队伍为空,所以他的到来没有影响到其他人,目前队伍为 [[7, 0]]
- 接下来走来了身高第二高之人,身高也是 7,他可以站在第一位哥们的前面或者后面,好的我们一起来看看他的选择:他选择了位置 1!为什么呢?因为 k 按照升序排列!所以虽然他身高也是 7,但是他站在了第一位哥们的后面。目前队伍:[[7, 0], [7, 1]]
- 接下来迎面走来的是第三个人,他的身高为 6,k 为 1,代表他前面只有 1 位比他高或者一样高的哥们,他挤了挤原先在位置 1 的老哥,因为老哥的身高为 7,比他高所以老哥往后挪了一个位置也没什么影响。目前队伍:[[7, 0], [6, 1], [7, 1]]
- 省略。。。
代码
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people, (a,b)->{
// if (a[0] == b[0]) return a[1] - b[1];
// return b[0] - a[0];
if(a[0] != b[0]) return b[0]-a[0]; //思想, 身高从大到小为逆序
return a[1]-b[1]; //思想, 再k从小到大顺序
});
List<int[]> queue = new LinkedList<>();
for(int[] item:people) {
queue.add(item[1], item);
}
return queue.toArray(new int[people.length][]); //语法
}
}
复杂度
- 时间: $$
- 空间: $$
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
动态规划(0-1背包)
思路
这道题可以变换为, 给一个数组, 其中的若干个数字之和是否等于该数组总加和的一半.
可以先列出几个明显的false的情况:
- 如果数组加和等于奇数, 则必定不可以
- 如果数组元素个数等于1, 则必定不可以
然后就可以用动态规划来做了, 动态规划方程为:
$dp[i][j]$的含义是数组[0,i]中是否有若干个数字之和等于j, 其中$i$的取值范围为$[0,n-1]$, $j$的取值范围是$[0,target]$.
$$
dp[i][j] =
\begin{cases}
dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]];(j>=nums[i]) \
dp[i][j] = dp[i-1][j];(j<nums[i])
\end{cases}
$$
初始条件是:
$$
dp[0…n][0] = true, 表示数组的任意i个之前的数字之后都可以等于0
$$
代码
class Solution {
public boolean canPartition(int[] nums) {
int length = nums.length;
int sum = 0;
for (int i = 0; i < length; i++) {
sum += nums[i];
}
//length < 2不可能
if (length < 2) return false;
//nums[]的和为奇数不可能
if (sum % 2 == 1) return false;
int target = sum / 2;
boolean[][] dp = new boolean[length][target + 1]; //dp[i][j]的含义是数组[0,i]中是否有若干个数字之和等于j //语法 思想
for(int i = 0; i < length; i++) {
dp[i][0] = true;
}
for (int i = 1; i < length; i++) {
for (int j = 0; j < target + 1; j++) {
if(j >= nums[i]) {
dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i]];
}else{
dp[i][j] = dp[i-1][j];
}
}
}
return dp[length-1][target];
}
}
复杂度
- 时间: $O(n*sum/2)$
- 空间: $O(n * sum/2)$
437. 路径总和 III
给定一个二叉树的根节点 root ,和一个整数 targetSum ,求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
路径 不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
前缀和
思路
前缀和的定义: 一个节点的前缀和就是该节点到根之间的路径和。
前缀和如何得出这道题的答案: (当前节点的前缀和 - targetNum)所对应的前缀和有几条线路, 就有几个答案
HashMap存的是什么: 以前缀和为key, 以该前缀和 所有的线路为value
状态恢复: 为什么要在遍历完节点之后, 将该节点的前缀和要不算进去
代码
class Solution {
Map<Long, Long> preSumMap; //以前缀和为key, 以该前缀和 所有的线路为value
Long target;
public int pathSum(TreeNode root, int targetSum){
preSumMap = new HashMap<>();
target = Long.valueOf(targetSum);
preSumMap.put(0L, 1L);
return recur(root, 0L).intValue();
}
private Long recur(TreeNode root, Long preSum){ //返回以root为根节点的符合题目条件的答案个数
if(root == null) return 0L;
Long curNum = Long.valueOf(root.val + preSum);
Long res = preSumMap.getOrDefault(Long.valueOf(curNum-target), 0L); //获取以该节点为最后一个节点符合题目的答案
preSumMap.put(Long.valueOf(curNum), preSumMap.getOrDefault(curNum, 0L)+1); //更新前缀和
res += recur(root.left, curNum); //得到以左孩子为根节点的符合题目的答案
res += recur(root.right, curNum);
preSumMap.put(Long.valueOf(curNum), preSumMap.get(curNum)-1); //状态恢复, 该节点遍历完之后的前缀和不应该再计算
return res;
}
}
复杂度
- 时间: $$
- 空间: $$
438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
异位词 指由相同字母重排列形成的字符串(包括相同的字符串)。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
滑动窗口
思路
先用一个数组(map)来计算字符串p的各个字符出现的次数, 然后设置一个滑动窗口, 来滑动字符串s的子串, 这个滑动窗口每向下滑动一次, 要减去被滑动出去的字符一次(i-1位置), 要加上被滑动进来的字符(i+pLen-1)一次, 然后比较新滑动窗口的子串和需要比较的字符串p的计数数组, 如果相等的话就等于.
代码
class Solution {
public List<Integer> findAnagrams(String s, String p) {
int sLen = s.length();
int pLen = p.length();
List<Integer> ans = new ArrayList<>();
if (sLen < pLen) return ans;
int [] sCount = new int[26]; //语法
int [] pCount = new int[26];
for(int i = 0; i < pLen; i++) {
++sCount[s.charAt(i)-'a'];
++pCount[p.charAt(i)-'a'];
}
if(Arrays.equals(sCount, pCount)) { //语法
ans.add(0);
}
for(int i = 1; i <= sLen-pLen; i++) { //思想,滑动到下标sLen-pLen
--sCount[s.charAt(i-1)-'a']; //思想,把i-1滑出去了, 所以要减去[i-1]这个字母
++sCount[s.charAt(i+pLen-1)-'a']; //思想,把i+pLen-1滑进去来了
if(Arrays.equals(sCount, pCount)) { //语法
ans.add(i);
}
}
return ans;
}
}
复杂度
- 时间:$O(m+(n−m)×Σ)$,其中 n 为字符串 s 的长度,m 为字符串 p 的长度,Σ 为所有可能的字符数。
- 空间: $O(Σ)$
448. 找到所有数组中消失的数字
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字,并以数组的形式返回结果。
示例 1:
输入:nums = [4,3,2,7,8,2,3,1]
输出:[5,6]
额外等长标志数组(self
思路
用一个额外的数组, 对于数组中的数字用作额外数组中的下标进行标记.
代码
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
int len = nums.length;
int [] flag = new int[len];
for(int i = 0; i < len; i++) {
flag[nums[i]-1] = 1;
}
List<Integer> ans = new ArrayList<>();
for(int i = 0; i < len; i++) {
if(flag[i] == 0) ans.add(i+1);
}
return ans;
}
}
复杂度
- 时间: $O(n), n为数组长度$,
- 空间: $O(n)$
原地哈希*
思路
对数组中的每个数字, 让对应下标上的数字变为负数, 这样最后扫描一下数组哪个位置上的数字为正数, 就说明该下标没出现过
代码
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
int len = nums.length;
for(int num:nums) {
int index = Math.abs(num)-1; //思想, 必须取绝对值, 因为数字可能已经被反转过了会出现负数
nums[index] = -Math.abs(nums[index]); //思想, 取绝对值后再取负
}
List<Integer> ans = new ArrayList<>();
for(int i = 0; i < len; i++) {
if(nums[i] > 0) ans.add(i+1);
}
return ans;
}
}
复杂度
- 时间: $O(n)$
- 空间: $O(n)$
461. 汉明距离
两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
输入:x = 1, y = 4
输出:2
解释:
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
位运算
思路
先异或, 然后再右移与1做与运算, 计数
代码
class Solution {
public int hammingDistance(int x, int y) {
int z = x ^ y;
int ans = 0;
for(int i = 0; i <32; i++) {
if((z & 1) == 1) ans = ans + 1;
z = z >> 1;
}
return ans;
}
}
复杂度
- 时间: $O(1)$
- 空间: $O(1)$
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-‘ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 '+' ,在 1 之前添加 '-' ,然后串联起来得到表达式 "+2-1" 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
回溯法
思路
- 回溯法是一种待优化的穷举法
- 回溯法的基本思想是在一棵含有问题全部可能解的状态空间树上进行深度优先搜索,解为叶子结点。搜索过程中,每到达一个结点时,则判断该结点为根的子树是否含有问题的解,如果可以确定该子树中不含有问题的解,则放弃对该子树的搜索,退回到上层父结点,继续下一步深度优先搜索过程。
- 在回溯法中,并不是先构造出整棵状态空间树,再进行搜索,而是在搜索过程,逐步构造出状态空间树,即边搜索,边构造。
代码
class Solution {
int count;
public int findTargetSumWays(int[] nums, int target) {
count = 0;
backTrack(nums, target, 0, 0); //下一个应该计算下标的0的位置, 并且和为0
return count;
}
//index: 下一个应该计算的位置, sum: 目前的和
private void backTrack(int[] nums, int target, int index, int sum) {
if(index == nums.length) { //思想
//到了最后的终点判断
if(sum == target) {
count++;
}
}else{
backTrack(nums, target, index+1, sum+nums[index]);//思想
backTrack(nums, target, index+1, sum-nums[index]);//思想
}
}
}
复杂度
- 时间: $O(2^n)$
- 空间: $O(n), n为递归栈的深度$
538. 把二叉搜索树转换为累加树
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
中序逆序遍历
思路
中序逆序遍历则就是一个由大到小的排列, 然后用一个全局变量存储每次遍历前的加和即可.
代码
class Solution {
int sum = 0; //思想
public TreeNode convertBST(TreeNode root) {
midTravel(root);
return root;
}
//反序中序遍历会得到一个由大到小的数字, 加和赋值即可
private void midTravel(TreeNode root) {
if(root == null) return;
midTravel(root.right);
sum += root.val; //思想
root.val = sum; //思想
midTravel(root.left);
}
}
复杂度
- 时间: $O(n), n为树的节点个数$
- 空间: $O(n), n为递归栈的最大深度, 最坏情况下为节点的个数$
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
问题转化
思路
问题可以转化成: 二叉树的 每个节点的左右子树的高度和+2 的最大值(+2是因为左右子树连接父节点也有两条边), 而在深度优先遍历求得树高的时候是得到过左右子树高度的。
我觉得这道题最妙的地点在于: 在深度遍历求得树高度的同时, 答案需要的左右子树高度都有, 所以能得到答案.
代码
class Solution {
int ans = 0;
private int depth(TreeNode root) {
if(root!=null) {
int leftHeight = depth(root.left);
int rightHeight = depth(root.right);
ans = Math.max(ans, leftHeight + rightHeight+2); //思想,根据左右子树高度得到答案
return Math.max(leftHeight, rightHeight) + 1; //思想,返回树的高度
}else{
return -1; //思想, 注意, 返回的是树的高度, null的高度应该算作-1
}
}
public int diameterOfBinaryTree(TreeNode root) {
depth(root);
return ans;
}
}
复杂度
- 时间: $O(n), n为节点的个数$
- 空间: $O(n),最坏情况下为n$
560. 和为 K 的子数组
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。
示例 1:
输入:nums = [1,1,1], k = 2
输出:2
前缀和+双重遍历(self
思路
先求每个位置的前缀和, 然后双重遍历,
第一重遍历到每个下标:
从这个下标起开始第二重遍历:
这个下标对应的前缀和 + k在后面出现了几次, 就计数几次.
另外如果这个下标的前缀和如果直接等于k, 则也要计数一次
代码
class Solution {
public int subarraySum(int[] nums, int k) {
int count = 0; //没有递归, 不用全局变量
for(int i = 1; i < nums.length; i++) {
nums[i] = nums[i-1] + nums[i]; //计算前缀和
}
for(int i = 0; i < nums.length; i++) {
int start = nums[i];
int end = k + start;
if(start == k) { //思想, 如果这个下标的前缀和等于目标数字, 直接计数一次
count++;
}
for (int j = i+1; j < nums.length; j++){
if(end == nums[j]) count++; //思想, 找符合start+k的前缀和的个数, 表明连续
}
}
return count;
}
}
复杂度
- 时间: $O(n^2, n为数组的大小)$
- 空间: $O(1)$
优化:
不关心具体的解的话, 求出前缀和的同时将前缀和用map来存储, 之后只要从map中提取前缀和出现的次数就可以了
581. 最短无序连续子数组
给你一个整数数组 nums ,你需要找出一个 连续子数组 ,如果对这个子数组进行升序排序,那么整个数组都会变为升序排序。
请你找出符合题意的 最短 子数组,并输出它的长度。
示例 1:
输入:nums = [2,6,4,8,10,9,15]
输出:5
解释:你只需要对 [6, 4, 8, 10, 9] 进行升序排序,那么整个表都会变为升序排序。
数学规律
思路
从左往右, 找到比左边最大值还小的最右下标, 从右往左, 找到比右边最小值还大的最左下标
代码
class Solution {
public int findUnsortedSubarray(int[] nums) {
int len = nums.length;
int max = nums[0];
int left = 0;
int right = 0;
int min = nums[len-1];
for(int i = 0; i < len; i++) {
if(nums[i] >= max) max = nums[i];
else right = i; //思想, 右索引是比numsB中最大元素的更小的最右边的那个(numsC比numsB都小)
if(nums[len-i-1] <= min) min = nums[len-i-1];
else left = len-i-1; //思想, 左索引是比numsB中最小元素的更大的最左边的那个(numsA比numsB都小)
}
return right!=0?right-left+1:0;
}
}
复杂度
- 时间: $O(n)$
- 空间: $O(1)$
排序比较
思路
将数组进行排序, 然后比较, 最左边的与原数组不相同的位置 和 最右边的与原数组不相同的位置.
617. 合并二叉树
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
递归(self
思路
就递归
代码
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1 == null && root2 == null) return null; //思想, 递归终止条件
TreeNode root = new TreeNode();
int root1_val = root1==null?0:root1.val;
int root2_val = root2==null?0:root2.val;
root.val = root1_val + root2_val;
TreeNode root_left = mergeTrees(root1==null?null:root1.left, root2==null?null:root2.left);
TreeNode root_right = mergeTrees(root1==null?null:root1.right, root2==null?null:root2.right);
root.left = root_left;
root.right = root_right;
return root;
}
}
621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。
然而,两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的 最短时间 。
脑筋急转弯
思路
最短时间和”冷却时间n”以及”计数最多的字符个数(tot)”有关:
$$
(n+1)×(max−1)+tot
$$
实际上,当任务总数不超过 (n+1)×(max−1)+tot 时,我们总能将其他任务插到空闲时间中去,不会引入额外的冻结时间(下左图);而当任务数超过该值时,我们可以在将其横向添加每个 n+1 块的后面,同时不会引入额外的冻结时间
所以, 最后就取两者之间的最大值
代码
class Solution {
public int leastInterval(char[] tasks, int n) {
int[] char_nums = new int[26]; //默认初始化为0
int max = 0;
for(char task:tasks){
char_nums[task-'A']++;
max = char_nums[task-'A'] > max ? char_nums[task-'A'] : max;
}
int count = 0;
for(int num:char_nums) {
if(num == max) count++;
}
return Math.max(tasks.length, (max-1)*(n+1)+count);
}
}
复杂度
- 时间: $O(n)$
- 空间: $O(1)$
647. 回文子串
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"
暴力枚举(self
思路
暴力枚举每一个子串是否是回文串
代码
class Solution {
public int countSubstrings(String s) {
int count = s.length(); //一位子串必定是回文串
for(int i = 2; i <= s.length(); i++) {
int num = countHelp(s, i);
//System.out.println(i + "-" + num);
count += num;
}
return count;
}
public int countHelp(String s, int n) {
//返回n位子串的回文子串的个数
int count = 0;
for (int i = 0; i <= s.length()-n; i++) { //思想
int start = i;
for(int j = 0; j < n/2; j++) { //判断是否是回文串
if(s.charAt(start+j)== s.charAt(start+n-1-j)) continue;
else {
count--;
break;
}
}
count++;
}
return count;
}
}
复杂度
- 时间: $O(n^3)$
- 空间: $O(1)$
递归
回溯
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
双重循环(self
单调栈
思路
用一个单调栈存储一个温度从大到小的下标, 遍历temperatures,
如果栈为空, 则入栈当前下标
如果当前位置比栈顶要大, 则不断出栈比当前位置小的元素的下标并且就能得到出栈下标位置的答案(i-top), 直到栈顶元素的下标对应的温度比当前位置对应的温度大(也就是温度从大到小的下标)
如果当前位置比栈顶要小, 则直接入栈
道理很好理解, 现在要找的是当前位置最近的比当前位置更大温度的距离, 用这种方法, 遍历当前位置, 对于栈里面比当前位置小的, 则可以用当前位置和栈里面存储的下标直接得出答案, 对于栈里面比当前位置温度大的, 则什么也不干, 入栈当前位置, 维护温度从大到小的下标即可.
代码
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int [] ans = new int[temperatures.length];
Stack<Integer> s = new Stack();
for (int i = 0; i < temperatures.length; i++) {
if(s.empty()) s.push(i);
else{
int top = s.peek();
while(temperatures[top] < temperatures[i]) {
ans[top] = i - top;
s.pop();
if(s.empty()) break;
else top = s.peek();
}
s.push(i);
}
}
return ans;
}
}
复杂度
- 时间: $O(n)$
- 空间: $O(n)$
欢迎在评论区中进行批评指正,转载请注明来源,如涉及侵权,请联系作者删除。

