08Leetcode每日一题

0开发 > Z刷题 Java

发布时间 : 2022-09-20 00:25

字数:2k 阅读 :

基础

Leetcode时间限制

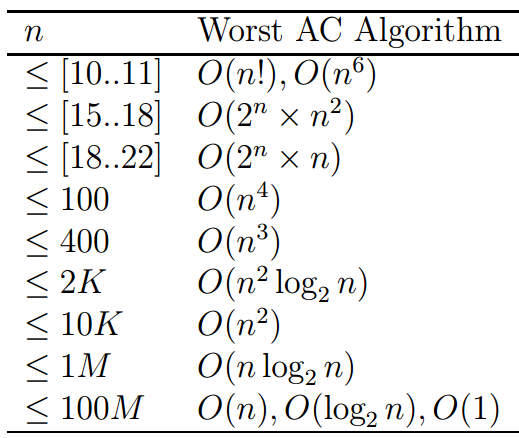
注意:

⏰表示未完成

⭐表示重要

🌟表示超级重要

😄表示我的思路并且通过了

😭表示自己尝试的方法但是通不过

🙆♂表示他人的方法通过了

🙅♂表示他人的方法但没通过

💭表示只写了想法没写代码无论自己或者其他人的.

题号.题目

描述

样例

思想1名称(self

思路

描述

代码

\\语法, 以后搜索\\语法可以学习语法
\\思想, 学习思想

复杂度

时间: $$
空间: $$

思想2名称*

思路

描述

代码

复杂度

时间: $$
空间: $$

每日一题

22-06-08 1037. 有效的回旋镖

给定一个数组 points ，其中 points[i] = [xi, yi] 表示 X-Y 平面上的一个点，如果这些点构成一个回旋镖则返回 true 。

回旋镖定义为一组三个点，这些点各不相同且不在一条直线上。

示例 1：

输入：points = [[1,1],[2,3],[3,2]]
输出：true

数学-叉乘的二维应用

思路

向量的叉乘的结果是一个向量, 模长是向量AB组成的平行四边形的面积, 向量方向垂直于AB组成的平面, 三维向量叉乘的计算公式:

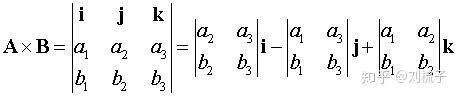
叉乘的扩展:
叉乘一般只定义在三维空间中, 但当其扩展到二维空间中, 其结论也很有用(将a3, b3都为0).
AXB = 0, 0, (a1b2-a2b1)k
此时(a1b2-a2b1)即为平行四边形的面积, 并且其一半就是AB向量组成的三角形的面积, 另外如果(a1b2-a2b1)>0, A正旋到B的角度<180, (a1b2-a2b1)<0则A正旋到B的角度>180,(a1b2-a2b1)=0则AB共线.

代码

class Solution {
    public boolean isBoomerang(int[][] points) {
        int delt_x12 = points[1][0]-points[0][0];
        int delt_x13 = points[2][0]-points[0][0];
        int delt_y12 = points[1][1]-points[0][1];
        int delt_y13 = points[2][1]-points[0][1];

        return delt_x12*delt_y13-delt_x13*delt_y12 != 0;	//思想
    }
}

复杂度

时间: $O(1)$
空间: $O(1)$

共点的三点斜率相同为一条直线

思路

只要计算两个点与另外一个点形成的斜率是否相同就好了, 但这里有坑,一个就是斜率的分母可能为0,所以有个技巧,就是$(c2-a2)/(c1-a1) == (b2-a2)/(b1-a1)$要变形为$(c2-a2)(b1-a1)==(b2-a2)(c1-a1)$

代码

class Solution {
    public boolean isBoomerang(int[][] points) {
        int delt_x12 = points[1][0]-points[0][0];
        int delt_x13 = points[2][0]-points[0][0];
        int delt_y12 = points[1][1]-points[0][1];
        int delt_y13 = points[2][1]-points[0][1];

        return delt_x12*delt_y13 != delt_x13*delt_y12;
    }
}

可以看到其实和向量的叉积一摸一样.

22-06-09 497. 非重叠矩形中的随机点

给定一个由非重叠的轴对齐矩形的数组 rects ，其中 rects[i] = [ai, bi, xi, yi] 表示 (ai, bi) 是第 i 个矩形的左下角点，(xi, yi) 是第 i 个矩形的右上角点。设计一个算法来随机挑选一个被某一矩形覆盖的整数点。矩形周长上的点也算做是被矩形覆盖。所有满足要求的点必须等概率被返回。

在给定的矩形覆盖的空间内的任何整数点都有可能被返回。

请注意，整数点是具有整数坐标的点。

实现 Solution 类:

Solution(int[][] rects) 用给定的矩形数组 rects 初始化对象。
int[] pick() 返回一个随机的整数点 [u, v] 在给定的矩形所覆盖的空间内。

前缀和+二分查找

思路

利用前缀和数组, 将所有可能取到的点的编号填写到前缀和数组中(数组下标作为长方形序号,数组内容作为长方形内点的序号的前缀和).

然后随机抽取一个数作为抽取到的点编号.

根据抽取到的点的编号用二分查找查询在哪个长方形中, 并且在长方形可能点的第几行第几列中, 再加上长方形左下角下标, 就知道具体的坐标了.

注意:

前缀和第0项是0, 接下来每一项存储的是前缀和, 所以是这样的结构

0 3 7 10 20

0 1 2 3 4
二分查找本应该在while循环外返回-1表示没有找到, 但是我们的二分查找找的是右端点, 也就是返回low.
random.nextInt(int n)可以等概率返回0-n之间的数.

0	3	7	10	20
0	1	2	3	4

代码

class Solution {

    Random random;
    ArrayList<Integer> rectPoints;
    int[][] rects;

    public Solution(int[][] rects) {
        //初始化
        this.random = new Random();
        this.rects = rects;
        this.rectPoints = new ArrayList<Integer>();

        //构造前缀和数组
        rectPoints.add(0);
        for(int[] rect:rects){
            int x_num = rect[2]-rect[0]+1;
            int y_num = rect[3]-rect[1]+1;
            rectPoints.add(rectPoints.get(rectPoints.size()-1)+x_num*y_num);
        }

    }
    
    public int[] pick() {
        int k = random.nextInt(rectPoints.get(rectPoints.size()-1));       //等概率抽取点下标, 点下标从0开始
        int rectIndex = binarySearch(rectPoints, k+1) - 1;        //k+1是因为前缀和存储的下标是从1开始的, -1是因为直接查找得到的是前缀和右端点, 而长方形的下标是左端点的下标.
        int rect_k = k - rectPoints.get(rectIndex);                         //rect_k是对应长方形中点的下标了
        int a = rects[rectIndex][0], b = rects[rectIndex][1], y = rects[rectIndex][3];
        int col = y - b + 1;        //长方形又多少列个可取点;
        int rect_row = rect_k / col;       //表示所抽取的随机点k在对应长方形可取点的哪一行;
        int rect_col = rect_k % col;       //表示所抽取的随机点k在对应长方形可取点的那一列;
        return new int[]{a+rect_row, b+rect_col};
    }
    private int binarySearch(ArrayList<Integer> arr, int target) {  //这里的target是抽取出的点坐标的前缀和对应的不是下标
        int low = 0, hign = arr.size()-1;
        while(low <= hign) {
            int mid = (hign-low) / 2 + low;
            int num = arr.get(mid);
            if(num < target) {
                low = mid + 1;
            }else if(num > target) {
                hign = mid - 1;
            }else{
                return mid;
            }
        }
        //return -1; 原本找不到的话返回-1表示找不到, 但是这里要用右端点前缀和的信息
        return low; //返回找不到的右端点, 恰好比target大
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(rects);
 * int[] param_1 = obj.pick();
 */

复杂度

时间: $构造函数复杂度为 O(n)，pick函数复杂度为 O(log⁡n)$
空间: $构造函数复杂度O(n), pick函数复杂度O(1)$

22-09-20 1636. 按照频率将数组升序排序

给你一个整数数组 nums ，请你将数组按照每个值的频率升序排序。如果有多个值的频率相同，请你按照数值本身将它们降序排序。

请你返回排序后的数组。

示例 1：

输入：nums = [1,1,2,2,2,3]
输出：[3,1,1,2,2,2]
解释：'3' 频率为 1，'1' 频率为 2，'2' 频率为 3 。

模拟:map+priorityQueue😄

思路

用map统计每个数字出现的次数, 然后遍历将每个map的项做成一个pair放入到优先队列中去, pair的key是数字, value是频次, 然后再出队入队遍历置每个数字为出现次数.

代码

class Solution {
    static Comparator<Pair<Integer, Integer>> cmp = new Comparator<Pair<Integer, Integer>>() {
      public int compare(Pair<Integer, Integer> e1, Pair<Integer, Integer> e2) {        //语法
        if(e1.getValue() != e2.getValue() ) return e1.getValue()-e2.getValue();
        else return e2.getKey()-e1.getKey();
      }
    };
    public int[] frequencySort(int[] nums) {

        Map<Integer, Integer> m = new HashMap<>();
        for(int i = 0; i < nums.length; i++) {
            m.put(nums[i], m.getOrDefault(nums[i],0)+1);
        }

        Queue<Pair<Integer, Integer>> q = new PriorityQueue<>(cmp);
        for (Map.Entry<Integer, Integer> entry : m.entrySet()) {                        //语法
            q.add(new Pair<Integer, Integer>(entry.getKey(), entry.getValue()));
        }   
        int index = 0;
        while(!q.isEmpty())
        {
            Pair<Integer, Integer> p = q.poll();                        //语法
            for (int i = 0; i < p.getValue(); i++) {
                nums[index++] = p.getKey();
            }
        }   
        return nums;
    }
}

复杂度

时间: $O(nlog^n)$
空间: $O(n)$

模拟:map+List排序🙆♂

代码

class Solution {
    public int[] frequencySort(int[] nums) {
        int n = nums.length;
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < n; i++) map.put(nums[i], map.getOrDefault(nums[i], 0) + 1);
        List<int[]> list = new ArrayList<>();
        for (int key : map.keySet()) list.add(new int[]{key, map.get(key)});//语法
        Collections.sort(list, (a, b)->{						//语法
            return a[1] != b[1] ? a[1] - b[1] : b[0] - a[0];
        });
        int[] ans = new int[n];
        int idx = 0;
        for (int[] info : list) {
            while (info[1]-- > 0) ans[idx++] = info[0];		//语法
        }
        return ans;
    }
}

22-09-21 854. 相似度为 K 的字符串 ⏰

欢迎在评论区中进行批评指正，转载请注明来源，如涉及侵权，请联系作者删除。